Algorytm Helda-Karpa
Algorytm Helda-Karpa (czasami określany jako algorytm Bellmana-Helda-Karpa) – algorytm służący do rozwiązywania problemu komiwojażera. Jest to algorytm dokładny oparty na programowaniu dynamicznym. Algorytm ma złożoność czasową O(n22n) i złożoność pamięciową O(n2n). Jest to co prawda złożoność gorsza od wielomianowej, ale algorytm ten jest znacznie lepszy od algorytmu sprawdzającego wszystkie warianty (złożoność czasowa O(n!)).
Działanie algorytmu
Załóżmy, że mamy graf liczący n wierzchołków ponumerowanych 1, 2, …, n. Wierzchołek 1 niech będzie wierzchołkiem początkowym. Jako di,j oznaczmy odległość między wierzchołkami i oraz j (są to dane wejściowe).
Oznaczmy jako D(S, p) optymalną długość ścieżki wychodzącej z punktu 1 i przechodzącej przez wszystkie punkty zbioru S tak, aby zakończyć się w punkcie p (p musi należeć do S). Przykładowo, zapis D({2, 5, 6}, 5) to optymalna długość ścieżki wychodzącej z punktu 1, przechodzącej przez punkty 2 i 6, kończącej się w punkcie 5. Liczbę punktów w zbiorze S oznaczmy jako s.
Wartość D(S, p) wyznaczamy następująco:
- Jeśli s=1, to D(S, p) = d1,p,
- Jeśli s>1, to D(S, p) = minx∈(S-{p})( D(S−{p}, x) + dx,p).
Mówiąc obrazowo, musimy za każdym razem ustalać, który punkt powinien być przedostatni na trasie (który punkt ma poprzedzać punkt p).
Na końcu wyznacza się rozwiązanie całego problemu. W tym celu należy znaleźć poprzednika punktu 1 korzystając ze wzoru: minx∈{2, …, n}( D({2, …, n}, x) + dx,1).
Przykład
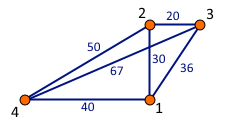
Dany jest graf zawierający cztery wierzchołki (taki, jak na ilustracji). Odległości między wierzchołkami są następujące:
- d1,2 = d2,1 = 30
- d1,3 = d3,1 = 36
- d1,4 = d4,1 = 40
- d2,3 = d3,2 = 20
- d2,4 = d4,2 = 50
- d3,4 = d4,3 = 67
Na początku wyznaczamy wartości D(S, p) dla jednoelementowych zbiorów S (s=1). Są to przypadki trywialne.
- D({2}, 2) = d1,2 = 30
- D({3}, 3) = d1,3 = 36
- D({4}, 4) = d1,4 = 40
Następnie wyznaczamy wartości D(S, p) dla dwuelementowych zbiorów S (s=2). W nawiasie kwadratowym zapisaliśmy numer przedostatniego węzła na ścieżce (węzła x dla optymalnego rozwiązania podproblemu). W tych przypadkach co prawda wybór jest oczywisty, gdyż zbiór S−{p} jest jednoelementowy, jednak już teraz pilnujmy notacji.
- D({2, 3}, 2) = min( D({3}, 3) + d3,2 ) = min(36 + 20) = min(56) = 56 [3]
- D({2, 3}, 3) = min( D({2}, 2) + d2,3 ) = min(30 + 20) = min(50) = 50 [2]
- D({2, 4}, 2) = min( D({4}, 4) + d4,2 ) = min(40 + 50) = min(90) = 90 [4]
- D({2, 4}, 4) = min( D({2}, 2) + d2,4 ) = min(30 + 50) = min(80) = 80 [2]
- D({3, 4}, 3) = min( D({4}, 4) + d4,3 ) = min(40 + 67) = min(80) = 107 [4]
- D({3, 4}, 4) = min( D({3}, 3) + d3,4 ) = min(36 + 67) = min(80) = 103 [3]
W kolejnych krokach wyznaczamy wartości D(S, p) dla trójelementowych zbiorów S (s=3).
- D({2, 3, 4}, 2) = min( D({3, 4}, 3) + d3,2, D({3, 4}, 4) + d4,2 ) = min(107 + 20, 103 + 50) = min(127, 153) = 127 [3]
- D({2, 3, 4}, 3) = min( D({2, 4}, 2) + d2,3, D({2, 4}, 4) + d4,3 ) = min(90 + 20, 80 + 67) = min(110, 147) = 110 [2]
- D({2, 3, 4}, 4) = min( D({2, 3}, 2) + d2,4, D({2, 3}, 3) + d3,4 ) = min(56 + 50, 50 + 67) = min(106, 117) = 106 [2]
Trójelementowy zbiór S jest dla tego zadania największym z możliwych, gdyż nie licząc wierzchołka początkowego mamy trzy wierzchołki. Możemy więc już teraz wyznaczyć rozwiązanie całego zadania:
- min( D({2, 3, 4}, 2) + d2,1, D({2, 3, 4}, 3) + d3,1, D({2, 3, 4}, 4) + d4,1,) = min(127 + 30, 110 + 36, 106 + 40) = min(157, 146, 146) = 146 [3]
Znamy już długość optymalnej trasy. Samą trasę możemy odtworzyć wykorzystując indeksy z kwadratowych nawiasów. Trasa to 1–3–2–4–1.
Złożoność obliczeniowa
Obliczmy, ile razy wyznaczana jest wartość D(S, p). Dla s=1 wartość tę wyznacza się n−1 razy. Dla każdego s z przedziału od 2 do n−1 rozważamy wszystkie s-elementowe kombinacje ze zbioru n−1-elementowego, przy czym dla każdej kombinacji rozważamy s wariantów punktu końcowego. Łącznie liczba wyznaczanych wartości D(S, p) wynosi zatem: $$(n-1)+∑↙{s=2}↖{n-1}s{(n-1)!}/{s!(n-1-s)!}$$ Korzystając z własności symbolu Newtona można przekształcić ten wzór do postaci: $$(n-1)2^{n-2}$$ Wartość D(S, p) wyznacza się w czasie liniowym (zakładając, że mamy bezpośredni dostęp do każdej zapamiętanej wartości, co można zapewnić prawidłowym indeksowaniem). Łącznie złożoność czasowa algorytmu wynosi więc O(n22n). Każdą wartość D(S, p) należy zapamiętać, zatem złożoność pamięciowa algorytmu to O(n2n).
Liczba głosów: 16.
Dodano: 7 sierpnia 2017 11:19, ostatnia edycja: 8 listopada 2017 16:03.
Zobacz też
Rekurencja (inaczej rekursja) – odwołanie się funkcji lub definicji do samej siebie. Mówiąc inaczej, podejście rekurencyjne polega na tym, że rozwiązanie problemu wyraża się za pomocą rozwiązania tego samego problemu dla mniejszych danych wejściowych. Stosowanie rekurencji jest charakterystyczne dla algorytmów projektowanych metodą dziel i zwyciężaj.
Typowym problemem, dla którego można zastosować rekurencję, jest obliczanie silni. Przypomnijmy, że silnia z n jest zdefiniowana jako n!=1×2×…×n. Funkcja ta może być równoważnie zapisana jako:
n!=(n−1)!×n, dla n>0,
n!=1, dla n=0.
W powyższym przykładzie górny wiersz jest ogólnym równaniem rekurencji, zaś dolny wiersz jest wartością brzegową. W języku C++ powyższa funkcja byłaby zapisana w poniższy sposób.
int silnia(int n)
{
if (n > 0)
{
return n * silnia(n-1);
}
else
{
return 1;
}
};
Przekształcenie postaci rekurencyjnej funkcji do postaci zwartej (tzn. takiej, która nie zawiera odwołania do samej siebie) jest określane jako rozwiązanie rekurencji. Metody rozwiązywania rekurencji są dostępne między innymi w książkach podanych w bibliografii.
Algorytmy stosujące rekurencję są zazwyczaj proste w implementacji. Jednocześnie wiążą się one z pewnymi problemami. Przy podejściu rekurencyjnym ta sama funkcja jest wywoływana wielokrotnie, co zużywa pamięć operacyjną (w skrajnych przypadkach może to spowodować przepełnienie stosu).
Metoda z zastosowaniem przepływu blokującego – algorytm wyznaczający maksymalny przepływ w sieci przepływowej. W algorytmie tym przepływ zwiększany jest iteracyjnie, w każdej iteracji wyznaczony przepływ jest powiększany o przepływ blokujący w warstwowej sieci residualnej.
Sortowanie przez wstawianie (ang. insertion sort) – prosty algorytm sortowania polegający na wstawianiu kolejnych elementów ciągu we właściwe miejsca. Złożoności czasowa algorytmu wynosi O(n2). Jest to algorytm realizujący metodę przyrostową.