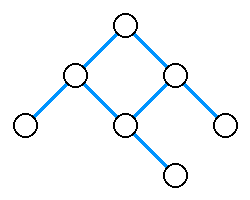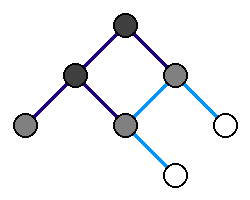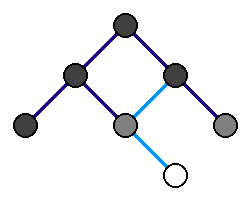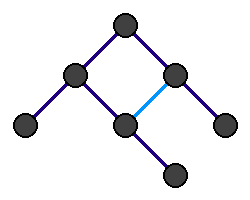
Przeszukiwanie wszerz
Przeszukiwanie wszerz (ang. breadth-first search, w skrócie BFS) – jeden z dwóch podstawowych algorytmów przeszukiwania grafu. Polega na przeglądaniu wierzchołków grafu według ich odległości od wierzchołka źródłowego (wyrażanej w liczbie krawędzi).
Przebieg algorytmu
- Oznacz wszystkie wierzchołki grafu jako nieodwiedzone.
- Odwiedź wierzchołek źródłowy, dodaj go do kolejki Q.
- Dopóki kolejka Q nie jest pusta:
- Pobierz pierwszy wierzchołek z kolejki (usuwając go z niej).
- Odwiedź wszystkie jeszcze nieodwiedzone wierzchołki sąsiednie tego wierzchołka, dodaj je do kolejki Q.
Zwyczajowo przyjmuje się, że:
- nieodwiedzone wierzchołki są oznaczone jako białe,
- odwiedzone wierzchołki znajdujące się w kolejce Q oznaczone są jako szare,
- odwiedzone wierzchołki spoza kolejki Q (te, których sąsiedzi są na pewno odwiedzeni) oznaczone są jako czarne.
Złożoność
Oznaczmy przez v liczbę wierzchołków grafu i przez e liczbę jego krawędzi. Początkowa część algorytmu ma złożoność O(v) – oznaczamy każdy wierzchołek. Liczba relacji sąsiedztwa jest równa liczbie krawędzi (lub jej dwukrotności, jeśli graf jest nieskierowany), więc złożoność czasowa głównej pętli algorytmu to O(e). Łącznie złożoność algorytmu jest więc rzędu O(v+e).
Jeśli każdy wierzchołek jest osiągalny ze źródła (po zakończeniu działania algorytmu nie będzie nieodwiedzonych wierzchołków), to e ≥ (v−1). Przy takim założeniu złożoność czasowa algorytmu wynosi O(e).
Zastosowanie
Za pomocą przeszukiwania grafu wszerz można wyznaczyć najkrótsze pod względem liczby krawędzi (ale nie wag!) ścieżki między wierzchołkiem źródłowym a pozostałymi wierzchołkami. Algorytm ten może być więc wykorzystany do rozwiązania szczególnego przypadku problemu najkrótszej ścieżki, gdy wszystkie krawędzie mają taką samą dodatnią wagę. Przeszukiwanie wszerz jest częścią składową niektórych bardziej zaawansowanych algorytmów grafowych, np. algorytmu Edmondsa-Karpa.
Bibliografia
- T.H. Cormen, Ch.E. Leiserson, R.L. Rivest, C. Stein, Wprowadzenie do algorytmów, Wydawnictwo Naukowe PWN, Warszawa, 2012, ISBN 9788301169114.


Liczba głosów: 3.
- Przeszukiwanie w głąb
- Przeszukiwanie wszerz
Dodano: 21 listopada 2017 17:35, ostatnia edycja: 30 stycznia 2019 15:55.
Zobacz też
Metoda przyrostowa – technika projektowania algorytmów polegająca na dodawaniu do rozwiązania kolejnych elementów z danych wejściowych. Przykładem algorytmu opartego na tej metodzie jest sortowanie przez wstawianie, gdzie kolejne elementy są wstawiane do posortowanej części tablicy.
Jest to metoda prosta, jednak sprawdza się tylko dla niektórych problemów obliczeniowych.
Matroid – struktura matematyczna składająca się z niepustego zbioru elementów E i takiej rodziny jego podzbiorów I, że spełnione są następujące warunki:
- Jeśli jakiś zbiór należy do I, to wszystkie jego podzbiory także należą do I.
- Jeśli weźmiemy dowolne dwa zbiory należące do I o różnej liczbie elementów, to jesteśmy w stanie dodać do mniejszego z nich taki element z większego (spośród tych, które nie należą do mniejszego), że utworzony w ten sposób zbiór także będzie należał do I.
Drugi warunek, zwany własnością wymiany, formalnie może być zapisany jako:
$$⋀↙{A,B∊I}↙{ |A|>|B| }⋁↙{t∊(A-B)} B∪\{t\} ∈ I$$Co istotne, rodzina zbiorów I nie musi zawierać wszystkich możliwych podzbiorów zbioru E. Ważne tylko, aby była spełniona własność wymiany. Przykładowo, dla E={a,b,c,d} prawidłową rodziną I, może być zarówno { {a,b}, {b,c}, {a}, {b}, {c}, ∅}, jak i { {a}, {b}, {c}, {d}, ∅}. Trywialnym przypadkiem poprawnego matroidu jest taki, w którym rodzina I zawiera jedynie zbiór pusty.
Algorytmy zachłanne (ang. greedy algorithms) – algorytmy podejmujące w każdym kroku taką decyzję, która w danej chwili wydaje się najkorzystniejsza. Inaczej mówiąc, algorytmy zachłanne dokonują zawsze wyborów lokalnie optymalnych licząc, że doprowadzi to do znalezienia rozwiązania globalnie optymalnego. W ogólnym przypadku algorytmy zachłanne nie zawsze znajdują rozwiązanie optymalne. Są one zatem podzbiorem algorytmów heurystycznych. Jednocześnie są to algorytmy deterministyczne – nie ma w nich losowości.
Bardzo prostym przykładem algorytmu zachłannego może być szukanie najwyższego punktu na określonym obszarze poprzez przesuwanie się zawsze w kierunku największego nachylenia (nigdy się nie cofając ani nie rozpatrując kilku wariantów drogi). Jak widać, w ten sposób prawdopodobnie dojdziemy do wierzchołka położonego najbliżej od punktu początkowego, który niekoniecznie będzie najwyższym.