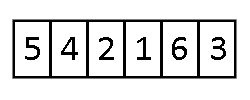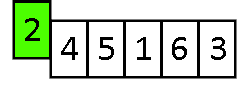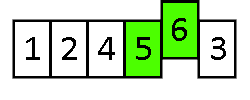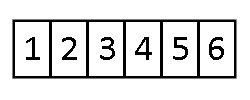Sortowanie przez wstawianie
Sortowanie przez wstawianie (ang. insertion sort) – prosty algorytm sortowania polegający na wstawianiu kolejnych elementów ciągu we właściwe miejsca. Złożoności czasowa algorytmu wynosi O(n2). Jest to algorytm realizujący metodę przyrostową.
Działanie algorytmu
Sortowany ciąg dzielony jest na część posortowaną i nieposortowaną. Na początku w części posortowanej znajduje się tylko jeden element (pierwszy). W każdym kolejnym kroku bierzemy pierwszy element z części nieposortowanej i wstawiamy we właściwe miejsce części posortowanej. Aby to zrobić, wstawiany element porównujemy kolejno z ostatnim elementem posortowanej części ciągu, z przedostatnim itd. Algorytm kończy się, gdy wszystkie elementy znajdują się w części posortowanej.
Przykładowy kod źródłowy w języku C jest umieszczony poniżej. Kod ten realizuje sortowanie rosnące.
void sortowanie_przez_wstawianie(int* tab, int n)
{
int i, j, t;
for (i = 1; i < n; ++i)
{
j = i;
while ( (j > 0) && (tab[j-1] > tab[j]) )
{
t = tab[j];
tab[j] = tab[j-1];
tab[j-1] = t;
--j;
}
}
}
Złożoność czasowa
Główna pętla algorytmu wykona się n-1 razy (n jest liczbą elementów do posortowania). W każdym wykonaniu pętli głównej wystąpi od 1 do j porównań, gdzie j jest numerem aktualnego wykonania pętli. W przypadku pesymistycznym algorytm wykona 1+…+(n-1)+(n-2)=(n-1)*n/2 porównań, czyli tyle samo, co algorytm sortowania bąbelkowego. Jednak w przypadku optymistycznym (sortowanie posortowanego ciągu) w każdym wykonaniu pętli głównej odbędzie się tylko jedno porównanie, co daje łącznie jedynie n-1 porównań (złożoność optymistyczna jest zatem liniowa).
Policzmy teraz, jaka jest średnia złożoność algorytmu. Jak już wspomniano, w każdym wykonaniu pętli głównej wystąpi od 1 do j porównań. Zakładając, że każda z tych liczb jest tak samo prawdopodobna, średnia liczba porównań wynosi (j+1)/2. W całym algorytmie wystąpi zatem (1+1)/2+(2+1)/2+…+n/2 porównań, czyli (n-1)(n+2)/4. Nadal jest to złożoność kwadratowa, jednak jest to algorytm szybszy od sortowania bąbelkowego. Przewaga sortowania przez proste wstawianie będzie tym większa, im większe będzie prawdopodobieństwo, że elementy w ciągu już na początku są częściowo posortowane.
Liczba głosów: 22.
- Bogosort
- Quicksort
- Sortowanie bąbelkowe
- Sortowanie przez scalanie
- Sortowanie przez wstawianie
Dodano: 29 września 2016 11:53, ostatnia edycja: 28 czerwca 2017 15:19.
Zobacz też
Metoda Otsu – algorytm służący do binaryzacji obrazu, czyli przekształcenia obrazu w odcieniach szarości do obrazu binarnego. Metoda ta realizuje progowanie globalne – dla całego obrazu wyznaczany jest jeden próg jasności, a następnie wszystkim pikselom jaśniejszym od tego progu przypisywana jest jedna wartość, a ciemniejszym druga.
Algorytm jest oparty na analizie histogramu. Przygotowanie histogramu polega na zliczeniu pikseli w każdym możliwym odcieniu (zazwyczaj liczba odcieni wynosi 256, gdyż tyle da się zakodować w jednym bajcie). Następnie należy sprawdzić każdy możliwy próg jasności i wybrać ten, dla którego wariancja międzyklasowa jest największa (lub suma ważona wariancji wewnątrzklasowych jest najmniejsza).
Jeśli obrazem wejściowym jest obraz kolorowy, można go łatwo sprowadzić do odcieni szarości. W przypadku kolorów zakodowanych w RGB najprostszym rozwiązaniem jest uśrednienie dla każdego piksela wartości wszystkich trzech kanałów.
Algorytm heurystyczny, heurystyka – algorytm niedający (w ogólnym przypadku) gwarancji znalezienia rozwiązania optymalnego, umożliwiający jednak znalezienie rozwiązania dość dobrego w rozsądnym czasie. Algorytmy tego typu używane są w takich problemach obliczeniowych, gdzie znalezienie rozwiązania optymalnego ma zbyt dużą złożoność obliczeniową (w szczególności są to problemy NP-trudne) lub w ogóle nie jest możliwe. Metody heurystyczne zaliczają się do sztucznej inteligencji.
Pojęcie algorytmów heurystycznych jest bardzo szerokie, dotyczy ono różnych technik projektowania algorytmów. Wiele heurystyk wykorzystuje losowość, inne zaś są deterministyczne (wówczas dla takich samych danych wejściowych algorytm zawsze zwróci ten sam wynik).
Ogólny algorytm heurystyczny (opisujący samą ideę poszukiwań) bywa określany w literaturze jako metaheurystyka. Zgodnie z tym nazewnictwem, metaheurystyką jest np. algorytm zachłanny (jako ogólna idea), zaś heurystyką jest np. algorytm najbliższego sąsiada (jako zastosowanie idei algorytmu zachłannego do konkretnego problemu).
Przykładowe techniki konstruowania algorytmów heurystycznych to:
- przeszukiwanie lokalne,
- algorytmy zachłanne,
- symulowane wyżarzanie,
- przeszukiwanie tabu,
- algorytmy genetyczne.
Algorytm Floyda-Warshalla – algorytm służący do wyznaczania najkrótszych ścieżek pomiędzy każdą parą wierzchołków w grafie. Jest to algorytm oparty na programowaniu dynamicznym. Algorytm ma złożoność czasową O(n3) i złożoność pamięciową O(n2), gdzie n jest liczbą wierzchołków.
Algorytm dopuszcza krawędzie o ujemnych wagach, o ile nie tworzą ujemnych cykli. Algorytm może być również wykorzystywany do wyszukiwania ujemnych cykli w grafie.