Algorytm najmniejszej krawędzi
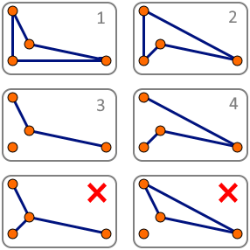(2) Przykład niespełnionej własności wymiany przy próbie przedstawiania problemu komiwojażera za pomocą matroidu. Nie da się do zbioru 3 dodać elementu zbioru 4 w taki sposób, aby uzyskać inny podzbiór poprawnego rozwiązania
Działanie algorytmu
Algorytm działa podobnie do algorytmu Kruskala poszukującego minimalnego drzewa rozpinającego. Polega on na kolejnym dołączaniu do rozwiązania najkrótszych spośród dopuszczalnych krawędzi. Działanie algorytmu można zapisać następująco:
- Posortuj wszystkie krawędzie rosnąco według ich wag, umieść je w kolejce.
- Pobierz z kolejki krawędź o najmniejszej wadze, usuń ją z kolejki.
- Sprawdź, czy dołączenie tej krawędzi do rozwiązania nie spowoduje utworzenia cyklu (nie dotyczy ostatniej iteracji) lub powstania wierzchołka, z którego wychodzą trzy krawędzie. Jeśli nie, dołącz krawędź do rozwiązania.
- Jeśli liczba krawędzi dołączonych do rozwiązania jest równa liczbie wierzchołków, zakończ działanie algorytmu. W przeciwnym razie przejdź do punktu 2.
Złożoność i ocena jakości
Główna pętla algorytmu wykona się maksymalnie n2 razy (n jest liczbą krawędzi). W trakcie każdego przebiegu pętli trzeba jednak sprawdzić, czy daną krawędź można dołączyć do rozwiązania. Złożoność obliczeniowa algorytmu zależy od sposobu implementacji sprawdzania tego warunku, a także od sposobu sortowania kolejki krawędzi. Według pracy [1] złożoność obliczeniowa algorytmu to O(n2log n).
Algorytm nie daje gwarancji znalezienia rozwiązania optymalnego. Jest on wprawdzie podobny do algorytmu Kruskala, jednak problemu komiwojażera (w odróżnieniu od problemu minimalnego drzewa rozpinającego) nie da się przedstawić za pomocą matroidu. Kontrprzykład został przedstawiony na rysunku (2). Według wspomnianej pracy [1], rozwiązania znalezione przez ten algorytm są średnio o ok. 16% gorsze od optymalnych.
Bibliografia
- D.S. Johnson, L.A. McGeoch, The Traveling Salesman Problem: A Case Study in Local Optimization, 1995 [Dostęp 2019-01-26].
- G. Gutin, A. Yeo, A. Zverovich, Traveling salesman should not be greedy: domination analysis of greedy-type heuristics for the TSP, Discrete Applied Mathematics, Volume 117, Issues 1–3, 2002, s. 81-86, DOI: 10.1016/S0166-218X(01)00195-0.
Liczba głosów: 3.
- 2-opt
- Algorytm Helda-Karpa
- Algorytm najbliższego sąsiada
- Algorytm najmniejszej krawędzi
- K-opt
- Powtarzalny algorytm najbliższego sąsiada
Dodano: 19 października 2016 19:21, ostatnia edycja: 24 kwietnia 2020 20:01.
Zobacz też
Algorytm – przepis, zbiór poleceń, opis ciągu operacji prowadzących do rozwiązania konkretnego problemu. Algorytm możemy również rozumieć jako funkcję przekształcającą dane wejściowe w dane wyjściowe.
Algorytm musi być skończony, czyli jego zapis ma składać się ze skończonej liczby znaków. Musi również być poprawny, czyli dla wszystkich możliwych danych wejściowych powinien zwracać prawidłowy wynik (może być nim informacja o braku rozwiązania). Algorytm musi wykazywać również własność stopu – niezależnie od danych wejściowych obliczenia algorytmu powinny dochodzić do punktu końcowego, czyli po prostu kończyć się (nie mogą np. wpadać w nieskończoną iterację). Zapis algorytmu musi być precyzyjny, bez jakichkolwiek niejasności.
Sortowanie – zagadnienie polegające na uporządkowaniu elementów zbioru rosnąco lub malejąco według pewnego klucza. Zagadnienie to, ze względu na częstość występowania, jest bardzo istotne dla informatyki. Istnieje wiele różnych algorytmów realizujących sortowanie.
Drzewo decyzyjne – metoda graficzna wspierająca podejmowanie decyzji, jak również model stosowany w uczeniu maszynowym do klasyfikacji lub regresji.
Podejmowanie decyzji z wykorzystaniem drzewa decyzyjnego odbywa się poprzez odpowiadanie na kolejne pytania. Pojedyncze pytanie musi być proste i dotyczyć jednego konkretnego atrybutu. Pytania ułożone są w strukturę hierarchiczną – wybór następnego pytania (lub końcowej decyzji) zależy od odpowiedzi udzielonej na poprzednie.
Proste drzewo decyzyjne może być w pełni zaprojektowane już przy tworzeniu programu i zaimplementowane w kodzie np. za pomocą instrukcji warunkowych. W uczeniu maszynowym drzewo jest generowane automatycznie na podstawie próbek ze zbioru uczącego.