Graf
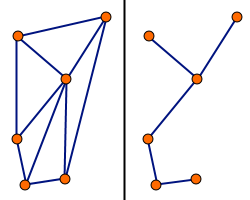
Graf – struktura składająca się ze zbioru wierzchołków oraz zbioru krawędzi. Grafy mają szerokie zastosowanie w informatyce, można za ich pomocą przedstawić wiele zagadnień.
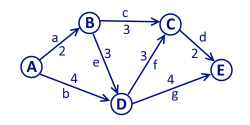
Wyróżniamy grafy nieskierowane oraz grafy skierowane. W grafie nieskierowanym relacja sąsiedztwa jest symetryczna, tzn. krawędź łączy wierzchołki „w obie strony”. W grafie skierowanym krawędzie są „jednokierunkowe”. Krawędź grafu skierowanego zazwyczaj jest określana jako łuk.
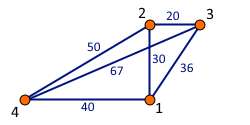
Graf ważony (inaczej graf z wagami) to taki graf, w którym każdej krawędzi przypisana jest pewna wartość liczbowa. Wartość ta może oznaczać np. długość krawędzi lub jej przepustowość.
Wybrane pojęcia związane z teorią grafów
- Trasa – ciąg kolejnych krawędzi, za pomocą którego możemy przejść z jednego wierzchołka grafu do innego (lub wrócić do tego samego).
- Ścieżka – trasa, w której każda krawędź występuje co najwyżej raz (mogą natomiast powtarzać się wierzchołki).
- Droga (ścieżka prosta) – trasa, w której każdy wierzchołek występuje co najwyżej raz. Wyjątkiem jest wierzchołek końcowy, który może być wierzchołkiem początkowym – taka ścieżka to cykl.
- Pętla – krawędź prowadząca z wierzchołka do niego samego.
- Krawędź wielokrotna – kilka krawędzi łączących tę samą parę wierzchołków.
- Graf prosty – graf nie zawierający żadnych pętli ani krawędzi wielokrotnych.
- Graf spójny – graf, w którym można wyznaczyć ścieżkę między każdą parą wierzchołków.
- Graf pełny – graf prosty, w którym każda para wierzchołków jest bezpośrednio połączona krawędzią.
- Drzewo – graf spójny nie mający żadnych cykli (taki, w którym między każdą parą wierzchołków można wyznaczyć dokładnie jedną ścieżkę).
Reprezentacja w pamięci komputera
W pamięci komputera grafy zazwyczaj są przechowywane w postaci list lub macierzy sąsiedztwa. W przypadku list sąsiedztwa każdemu wierzchołkowi przyporządkowana jest lista wierzchołków z nim sąsiadujących. W przypadku macierzy sąsiedztwa w pamięci przechowywana jest macierz, w której każdy wiersz i każda kolumna odpowiada innemu wierzchołkowi. Liczba na przecięciu wiersza i kolumny informuje, ile krawędzi łączy daną parę wierzchołków (w przypadku grafu ważonego prostego można tam zamieścić wagę krawędzi). W przypadku grafu nieskierowanego macierz jest symetryczna.
Bibliografia
- R.J. Wilson, Wprowadzenie do teorii grafów, Wydawnictwo Naukowe PWN, Warszawa, 2012, ISBN 9788301150662.
Liczba głosów: 0.
Dodano: 6 grudnia 2017 10:31, ostatnia edycja: 30 stycznia 2019 15:58.
Zobacz też
Ten artykuł opisuje algorytm rozwiązujący problem wydawania reszty oparty na programowaniu dynamicznym. Algorytm ten daje gwarancję znalezienia rozwiązania optymalnego.
Istnieje również pewna modyfikacja tego algorytmu, która została opisana w osobnym artykule.
Wyznaczanie maksymalnego przepływu – problem obliczeniowy polegający na wyznaczeniu maksymalnego przepływu w sieci przepływowej.
Sieć przepływowa jest skierowanym grafem prostym. Każdy łuk (krawędź skierowana w grafie) ma swoją nieujemną wagę, która oznacza maksymalny dopuszczalny przepływ w tym łuku. Na potrzeby tego artykułu nazwijmy rzeczy przepływające przez sieć danymi. Jeden z wierzchołków sieci jest źródłem, z którego wypływają przesyłane dane. Inny z wierzchołków to ujście, do którego te dane wpływają. Zakłada się ponadto, że dla każdego z pozostałych wierzchołków istnieje ścieżka ze źródła do ujścia przechodząca przez ten wierzchołek.
Przepływem w sieci nazywamy przyporządkowanie każdemu łukowi pewnej wartości, która oznacza liczbę danych aktualnie przesyłanych przez ten łuk. Wartości te muszą spełniać następujące warunki:
- Wartość przyporządkowana krawędzi musi być mniejsza lub równa jej wadze (warunek przepustowości).
- Do każdego wierzchołka (poza źródłem i ujściem) musi wpływać tyle samo danych, ile z niego wypływa (warunek zachowania przepływu).
Omawiany problem polega na dobraniu takiego przepływu, aby liczba danych wypływających ze źródła (i zarazem wpływających do ujścia) była jak największa.
Symulowane wyżarzanie – jedna z technik projektowania algorytmów heurystycznych (metaheurystyka). Cechą charakterystyczną tej metody jest występowanie parametru sterującego zwanego temperaturą, który maleje w trakcie wykonywania algorytmu. Im wyższą wartość ma ten parametr, tym bardziej chaotyczne mogą być zmiany. Podejście to jest inspirowane zjawiskami obserwowanymi w metalurgii – im większa temperatura metalu, tym bardziej jest on plastyczny.
Jest to metoda iteracyjna: najpierw losowane jest pewne rozwiązanie, a następnie jest ono w kolejnych krokach modyfikowane. Jeśli w danym kroku uzyskamy rozwiązanie lepsze, wybieramy je zawsze. Istotną cechą symulowanego wyżarzania jest jednak to, że z pewnym prawdopodobieństwem może być również zaakceptowane rozwiązanie gorsze (ma to na celu umożliwienie wyjście z maksimum lokalnego).
Prawdopodobieństwo przyjęcia gorszego rozwiązania wyrażone jest wzorem e(f(X)−f(X'))/T (rozkład Boltzmanna), gdzie X jest poprzednim rozwiązaniem, X' nowym rozwiązaniem, a f funkcją oceny jakości – im wyższa wartość f(X), tym lepsze rozwiązanie. Ze wzoru można zauważyć, że prawdopodobieństwo przyjęcia gorszego rozwiązania spada wraz ze spadkiem temperatury i wzrostem różnicy jakości obu rozwiązań.