2-opt
Przykład wykonania algorytmu
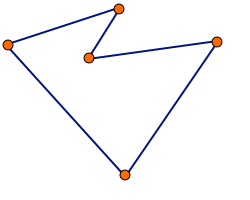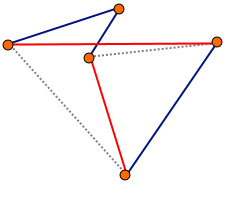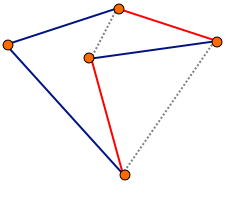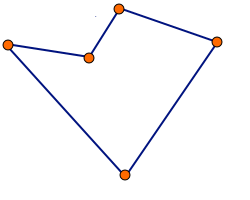
2-opt, algorytm 2-optymalny – algorytm lokalnej optymalizacji wykorzystywany przy rozwiązywaniu problemu komiwojażera. Jest to szczególny przypadek algorytmu k-optymalnego.
Algorytm 2-opt nie służy do wyznaczania trasy, a jedynie do ulepszania jej. Samą trasę można wyznaczyć np. za pomocą algorytmu najbliższego sąsiada. Algorytm może być wykorzystany do ulepszenia algorytmu genetycznego – w ten sposób powstanie algorytm memetyczny.
Działanie algorytmu
Algorytm 2-opt polega na usunięciu z cyklu dwóch krawędzi i zastąpieniu ich innymi krawędziami tak, aby utworzyć inny cykl. Czynność jest powtarzana dla każdej pary krawędzi, z wyjątkiem krawędzi sąsiadujących ze sobą – ich modyfikacja nie spowodowałaby żadnych zmian. Za każdym razem modyfikujemy cykl początkowy (nie rozwiązanie z poprzedniego kroku). Po sprawdzeniu wszystkich par krawędzi sprawdzamy, która modyfikacja najbardziej skróciła trasę. Jeśli żadna modyfikacja nie poprawiła trasy, zwracamy cykl początkowy (nie zmieniamy nic).
Algorytm można wykonywać kilkakrotnie, aż do momentu, w którym żadna modyfikacja nie spowoduje skrócenia trasy. W ten sposób osiągnięte zostanie minimum lokalne.
Złożoność obliczeniowa
W trakcie jednego przebiegu algorytmu trzeba przeanalizować n*(n-3)/2 par krawędzi. Złożoność czasowa (jednej iteracji) wynosi więc O(n2).
Bibliografia
- D.S. Johnson, L.A. McGeoch, The Traveling Salesman Problem: A Case Study in Local Optimization (link) [dostęp: 3 czerwca 2017].
Liczba głosów: 0.
Dodano: 3 czerwca 2017 15:05, ostatnia edycja: 17 czerwca 2017 16:09.
Zobacz też
Problem komiwojażera (ang. travelling salesman problem, w skrócie TSP) – problem obliczeniowy polegający na poszukiwaniu w grafie takiego cyklu, który zawiera wszystkie wierzchołki (każdy dokładnie raz) i ma jak najmniejszy koszt. Bardziej formalnie, problem komiwojażera polega na poszukiwaniu w grafie cyklu Hammiltona o najmniejszej wadze.
Problem ma liczne zastosowania w życiu codziennym. Najlepszym przykładem jest praca kuriera, który musi wyjechać z magazynu, zawieźć przesyłki w różne miejsca i wrócić do magazynu.
Nie jest znany efektywny (tj. działający w czasie co najwyżej wielomianowym) algorytm dający gwarancję znalezienia optymalnego rozwiązania problemu komiwojażera. Problem ten jest bowiem zaliczany do klasy problemów NP-trudnych. W wersji decyzyjnej (czy istnieje cykl o długości mniejszej od x) problem jest zaliczany do klasy problemów NP-zupełnych. W grafie pełnym mającym n wierzchołków liczba możliwych cykli Hammiltona wynosi aż (n-1)!/2. W praktyce sprawdzenie wszystkich możliwości jest zatem wykonalne tylko dla niewielkiej liczby wierzchołków.
Metoda przyrostowa – technika projektowania algorytmów polegająca na dodawaniu do rozwiązania kolejnych elementów z danych wejściowych. Przykładem algorytmu opartego na tej metodzie jest sortowanie przez wstawianie, gdzie kolejne elementy są wstawiane do posortowanej części tablicy.
Jest to metoda prosta, jednak sprawdza się tylko dla niektórych problemów obliczeniowych.
Ten artykuł opisuje pewną modyfikację algorytmu opartego na programowaniu dynamicznym rozwiązującego problem wydawania reszty. Algorytm ten daje gwarancję znalezienia rozwiązania optymalnego. Algorytm zaproponował J.W. Wright w pracy The Change-Making Problem (link w bibliografii).