K-opt
K-opt, algorytm k-optymalny – algorytm lokalnej optymalizacji wykorzystywany przy rozwiązywaniu problemu komiwojażera. Algorytm ten nie służy do samego wyznaczania trasy, a jedynie do ulepszania jej. Najprostszą wersją tego algorytmu jest algorytm 2-optymalny.
Działanie algorytmu
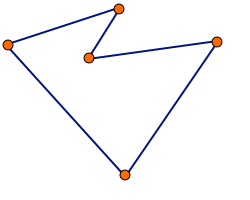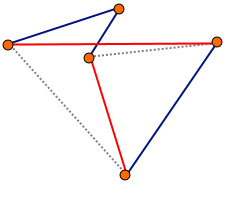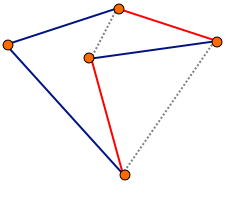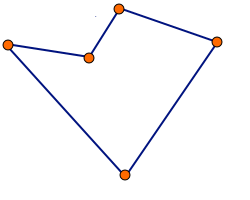
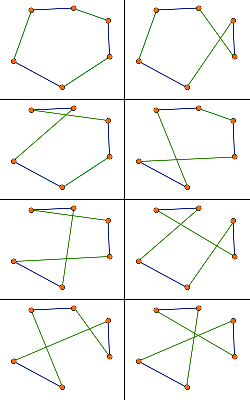
Algorytm polega na usuwaniu z cyklu k krawędzi i zastępowaniu ich innymi krawędziami tak, aby utworzyć inny prawidłowy cykl. Jeśli osiągnięte w ten sposób rozwiązanie jest lepsze od dotychczas znalezionego, zapamiętujemy je. Za każdym razem modyfikujemy cykl początkowy (nie rozwiązanie z poprzedniego kroku).
Usunięcie z cyklu k krawędzi sprawia, że cykl zostaje podzielony na k fragmentów. Należy sprawdzić wszystkie możliwości połączenia tych fragmentów w całość. Taki krok algorytmu należy powtórzyć dla każdej k-elementowej grupy krawędzi.
Algorytm można wykonywać kilkakrotnie, aż do momentu, w którym żadna modyfikacja nie spowoduje skrócenia trasy. W ten sposób osiągnięte zostanie minimum lokalne.
Złożoność obliczeniowa
Załóżmy, że mamy cykl liczący n krawędzi. Jeśli chcemy usunąć z niego k krawędzi, to możemy uczynić to na n!/(k!(n-k)!) sposobów (kombinacja z n po k). Dla każdej kombinacji musimy sprawdzić wszystkie możliwości połączenia fragmentów cyklu w inny sposób. Fragmenty te możemy ustawić w różnej kolejności na (k-1)! sposobów. Dodatkowo każdy fragment można odwrócić, czyli wartość tę musimy pomnożyć przez 2k-1. Jest to oszacowanie z pewnym nadmiarem – jeśli dany fragment jest jednoelementowy, to nie trzeba go odwracać (im większe k, tym więcej będzie takich elementów, zatem dla dużych k czynnik ten będzie zanikał).
Podsumowując, mamy do sprawdzenia maksymalnie n!2k-1/(k(n-k)!) wariantów. Jest to złożoność rzędu O(nk), przy czym nawet dla dużych k złożoność nie przekroczy n!.
Biorąc pod uwagę, że złożoność algorytmu w zależności od k jest wykładnicza, w praktyce używa się tylko niewielkich wartości k, zazwyczaj 2 lub 3. Dla k=n wykonanie algorytmu byłoby tożsame ze sprawdzeniem wszystkich możliwych rozwiązań problemu komiwojażera.
Liczba głosów: 5.
Dodano: 17 czerwca 2017 15:20, ostatnia edycja: 17 czerwca 2017 16:08.
Zobacz też
Algorytmy zachłanne (ang. greedy algorithms) – algorytmy podejmujące w każdym kroku taką decyzję, która w danej chwili wydaje się najkorzystniejsza. Inaczej mówiąc, algorytmy zachłanne dokonują zawsze wyborów lokalnie optymalnych licząc, że doprowadzi to do znalezienia rozwiązania globalnie optymalnego. W ogólnym przypadku algorytmy zachłanne nie zawsze znajdują rozwiązanie optymalne. Są one zatem podzbiorem algorytmów heurystycznych. Jednocześnie są to algorytmy deterministyczne – nie ma w nich losowości.
Bardzo prostym przykładem algorytmu zachłannego może być szukanie najwyższego punktu na określonym obszarze poprzez przesuwanie się zawsze w kierunku największego nachylenia (nigdy się nie cofając ani nie rozpatrując kilku wariantów drogi). Jak widać, w ten sposób prawdopodobnie dojdziemy do wierzchołka położonego najbliżej od punktu początkowego, który niekoniecznie będzie najwyższym.
Quicksort, sortowanie szybkie – algorytm sortowania działający w średnim przypadku w czasie liniowo-logarytmicznym. Algorytm jest oparty na metodzie dziel i zwyciężaj. Nie jest to algorytm stabilny ani wykazujący zachowanie naturalne, jednak ze względu na efektywność jest algorytmem bardzo popularnym.
Powtarzalny algorytm najbliższego sąsiada (ang. repetitive nearest neighbour algorithm, w skrócie RNN) – algorytm służący do rozwiązywania problemu komiwojażera korzystający z algorytmu najbliższego sąsiada.
Algorytm polega na wielokrotnym wykonaniu algorytmu najbliższego sąsiada w taki sposób, aby każdy wierzchołek raz był wierzchołkiem początkowym. Następnie algorytm zwraca najlepsze spośród otrzymanych rozwiązań.
Dla grafu pełnego algorytm ma złożoność O(n3), gdzie n jest liczbą wierzchołków. W trakcie wykonywania algorytmu RNN n razy zostanie wykonany algorytm najbliższego sąsiada, który ma złożoność czasową O(n2).
Algorytm RNN nie daje gwarancji znalezienia rozwiązania optymalnego. W odróżnieniu od algorytmu najbliższego sąsiada daje jednak gwarancję, że zwróci rozwiązanie co najmniej tak dobre, jak n/2-1 innych rozwiązań (dowód i więcej informacji na ten temat znajduje się w pracy podanej w bibliografii).