Problem wydawania reszty (programowanie dynamiczne, drugi wariant)

Ten artykuł opisuje pewną modyfikację algorytmu opartego na programowaniu dynamicznym rozwiązującego problem wydawania reszty. Algorytm ten daje gwarancję znalezienia rozwiązania optymalnego. Algorytm zaproponował J.W. Wright w pracy The Change-Making Problem (link w bibliografii).

Sformułowanie problemu

Dany jest posortowany rosnąco ciąg nominałów A=(c₁, c₂, …, c_n) oraz kwota do wydania r. Należy wyznaczyć takie nieujemne współczynniki k₁, k₂, …, k_n, że k₁c₁+k₂c_c+…+k_nc_n=r, a suma k₁+k₂+…+k_n jest jak najmniejsza.

Zakładamy, że wszystkie nominały i kwota r są liczbami naturalnymi, a nominał c₁=1. Przyjmujemy również że wartości k nie mają górnych ograniczeń.

Opis algorytmu

Ten algorytm polega na rozstrzyganiu, od którego z nominałów należy rozpocząć wydawanie kwoty. Oznaczmy jako o_i optymalną (najmniejszą z możliwych) liczbę monet potrzebnych do wyznaczenia kwoty i. Aby wyznaczyć wartość o_i musimy wiedzieć, która z wartości: o_i-c1, o_i-c2, … ,o_i-cj jest najmniejsza (j jest indeksem najwyższego nominału mniejszego bądź równego i). Rozwijając to zagadnienie rekurencyjnie dojdziemy w końcu do przypadku oczywistego, jakim jest wydanie kwoty 0 za pomocą 0 monet. Formalnie możemy to zapisać jako:

o_i =

• 0 dla i=0
• min(o_i-c1, o_i-c2, … ,o_i-cj)+1 dla i>0 i c₁, c₂, …, c_j ≤ i

Warto zauważyć, że w ten sposób wyznaczamy jedynie łączną liczbę potrzebnych monet, a nie poszczególne współczynniki k_i. Dlatego też w każdej komórce tabeli oprócz wartości o_i należy zapamiętać również wartość s_i przechowującą indeks nominału, od którego należy rozpocząć wydawanie kwoty i.

Mając wyznaczone wartości s_i poszczególne współczynniki k_i można wyznaczyć w prosty sposób. Na początku wszystkim współczynnikom k_i przypisujemy wartość 0. Następnie sprawdzamy wartość s_r i zwiększamy wartość współczynnika k_sr o 1. W kolejnym kroku zmniejszamy wartość r o c_sr i odczytujemy kolejną wartość s_r. Czynności powtarzamy, dopóki r>0.

Wartości o_i można wyznaczać rekurencyjnie, jednak częściej wypełnia się ją w sposób iteracyjny (od wartości o₀ do o_r).

Złożoność obliczeniowa

Tabela tworzona w trakcie wykonywania algorytmu ma r+1 komórek (r jest kwotą do wydania). W trakcie wypełniania każdej komórki musimy sprawdzić co najwyżej n możliwości (n jest liczbą nominałów). Złożoność czasowa algorytmu jest zatem O(nr), a złożoność pamięciowa to O(r).

Przykład

Załóżmy, że chcemy wyrazić kwotę 6 mając monety o nominałach 1, 3 i 4. Aby wyrazić tę kwotę za pomocą jak najmniejszej liczby monet, musimy wiedzieć, od której monety najlepiej zacząć wydawanie kwoty. W naszym przypadku musimy zatem wiedzieć:

• Ile monet potrzeba do wydania kwoty 2? (6-4=2)
• Ile monet potrzeba do wydania kwoty 3? (6-3=3)
• Ile monet potrzeba do wydania kwoty 5? (6-1=5)

Aby odpowiedzieć na powyższe pytania, musimy rekurencyjnie stawiać kolejne, aż dojdziemy do przypadku oczywistego (kwota równa 0 wymagająca użycia 0 monet). Aby nie stosować rekurencji, rozwiążmy problem w sposób iteracyjny, wyznaczając liczby monet potrzebnych do wydania kolejnych kwot od 0 do 6.

• Aby wydać kwotę 0, potrzebujemy 0 monet (przypadek oczywisty).
• Aby wydać kwotę 1, musimy użyć monety o nominale 1.
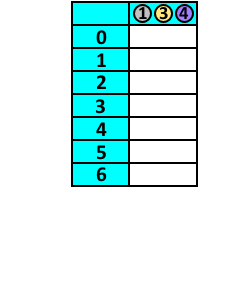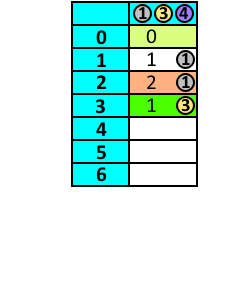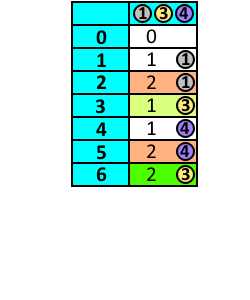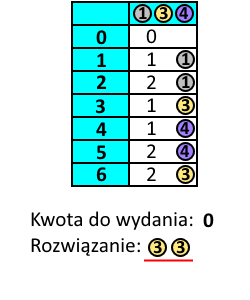
• Aby wydać kwotę 2, musimy użyć monety o nominale 1. Zostaje wówczas do wydania kwota 1, do wydania której potrzeba 1 monety. Łącznie do wydania kwoty 2 potrzebujemy zatem 2 monet.
• Aby wydać kwotę 3, możemy użyć monety o nominale 1 (wówczas pozostaje kwota 2 wymagająca użycia 2 monet) albo monety o nominale 3 (wówczas pozostaje kwota 0 wymagająca użycia 0 monet). Używamy więc monety o nominale 3. Do wydania kwoty 2 potrzebujemy zatem 1 monety.
• Aby wydać kwotę 4, możemy użyć monety o nominale 1 (wówczas pozostaje kwota 3 wymagająca użycia 1 monety), monety o nominale 3 (wówczas pozostaje kwota 1 wymagająca użycia 1 monety) albo monety o nominale 4 (wówczas pozostaje kwota 0 wymagająca użycia 0 monet). Używamy więc monety o nominale 3. Do wydania kwoty 4 potrzebujemy zatem 1 monety.
• Aby wydać kwotę 5, możemy użyć monety o nominale 1 (wówczas pozostaje kwota 4 wymagająca użycia 1 monety), monety o nominale 3 (wówczas pozostaje kwota 2 wymagająca użycia 2 monet) albo monety o nominale 4 (wówczas pozostaje kwota 1 wymagająca użycia 1 monety). Używamy więc monety o nominale 4. Do wydania kwoty 5 potrzebujemy zatem 2 monet.
• Aby wydać kwotę 6, możemy użyć monety o nominale 1 (wówczas pozostaje kwota 5 wymagająca użycia 2 monet), monety o nominale 3 (wówczas pozostaje kwota 3 wymagająca użycia 1 monety) albo monety o nominale 4 (wówczas pozostaje kwota 2 wymagająca użycia 2 monet). Używamy więc monety o nominale 3. Do wydania kwoty 6 potrzebujemy zatem 2 monet.

Podsumowując, aby wydać kwotę 6 najpierw należy użyć monety o nominale 3. Pozostaje wówczas kwota 3, do wydania której ponownie używamy monety o nominale 3. Uzyskujemy w ten sposób rozwiązanie optymalne.

Kod źródłowy

Przykładowa implementacja algorytmu w języku C++ jest dostępna poniżej.

void programowanieDynamiczne(int* c, int n, int r, int* k) {

	// Alokacja tymczasowych tabel
	int* o = new int[r+1]; // Tutaj będą optymalne liczby monet potrzebne do wydania kwoty "i"
	int* s = new int[r+1]; // Tutaj będą indeksy nominałów, od których należy rozpocząć wydawanie kwoty "i"

	int i, j, opt; // Liczniki, zmienna pomocnicza

	o[0] = s[0] = 0; // Inicjalizacja dla kwoty 0

	// Wypełnianie tabel
	for (i = 1; i <= r; ++i) {

		opt = 0;

		for (j = 1; j < n; ++j) {

			if ( (c[j] <= i) && (o[i - c[j]] <= o[i - c[opt]])) {
				opt = j;
			}
		}

		o[i] = o[i - c[opt]] + 1;
		s[i] = opt;

	}

	// Wyzerowanie tablicy k[]
	for (j = 0; j < n; ++j) {
		k[j] = 0;
	}

	// Zwiększanie wartości k na podstawie tablicy s
	while (r > 0) {
		k[s[r]] += 1;
		r -= c[s[r]];
	}

	// Zwolnienie pamięci
	delete[] o;
	delete[] s;

}

Przykładowe wywołanie funkcji:

int main()
{
	int n = 6;
	int a[6] = { 1, 3, 4, 10, 30, 40 };
	int k[6] = { 0 };
	int r = 56;

	programowanieDynamiczne(a, n, r, k);

	return 0;
}

Bibliografia

1. J.W. Wright, The Change-Making Problem (link) [dostęp: 25 listopada 2016]