Programowanie dynamiczne
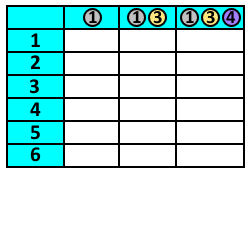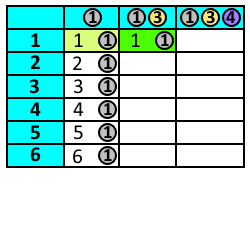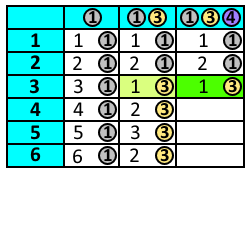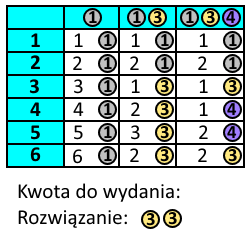
Programowanie dynamiczne – technika projektowania algorytmów polegająca na rozwiązywaniu podproblemów i zapamiętywaniu ich wyników. W technice tej, podobnie jak w metodzie dziel i zwyciężaj, problem dzielony jest na mniejsze podproblemy. Wyniki rozwiązywania podproblemów są jednak zapisywane w tabeli, dzięki czemu w przypadku natrafienia na ten sam podproblem nie trzeba go ponownie rozwiązywać.
Wykorzystując programowanie dynamiczne można zastosować metodę zstępującą z zapamiętywaniem lub metodę wstępującą.
- Metoda zstępująca z zapamiętywaniem polega na rekurencyjnym wywoływaniu funkcji z zapamiętywaniem wyników. Metoda ta jest podobna do metody dziel i zwyciężaj – różni się od niej tym, że jeśli rozwiązanie danego problemu jest już w tabeli z wynikami, to należy je po prostu stamtąd odczytać.
- Metoda wstępująca polega na rozwiązywaniu wszystkich możliwych podproblemów, zaczynając od tych o najmniejszym rozmiarze. Wówczas w momencie rozwiązywania podproblemu na pewno są już dostępne rozwiązania jego podproblemów. W tym podejściu nie zużywa się pamięci na rekurencyjne wywołania funkcji. Może się jednak okazać, że część podproblemów została rozwiązana nadmiarowo (nie były one potrzebne do rozwiązania głównego problemu).
Własność optymalnej podstruktury
Programowanie dynamiczne jest stosowane do rozwiązywania problemów, które wykazują własność optymalnej podstruktury. Własność ta oznacza, że optymalne rozwiązanie problemu jest funkcją optymalnych rozwiązań podproblemów (czyli znając optymalne rozwiązania podproblemów można efektywnie wyznaczyć rozwiązanie problemu).
Przykłady algorytmów
Przykładowe algorytmy oparte na programowaniu dynamicznym to:
Zobacz też
Bibliografia
- T.H. Cormen, Ch.E. Leiserson, R.L. Rivest, C. Stein, Wprowadzenie do algorytmów, Wydawnictwo Naukowe PWN, Warszawa, 2012, ISBN 9788301169114.
Liczba głosów: 6.
- Algorytmy heurystyczne
- Dziel i zwyciężaj
- Metoda przyrostowa
- Programowanie dynamiczne
Dodano: 1 lipca 2017 14:22, ostatnia edycja: 30 stycznia 2019 15:52.
Zobacz też
Algorytm Johnsona – algorytm służący do wyznaczania najkrótszych ścieżek pomiędzy każdą parą wierzchołków w grafie. Algorytm wykorzystuje algorytm Dijkstry i algorytm Bellmana-Forda. Dopuszcza krawędzie o ujemnych wagach, o ile nie tworzą ujemnych cykli.
Złożoność czasowa algorytmu (jeśli algorytm Dijkstry zostanie zaimplementowany z wykorzystaniem kopca Fibonacciego) to O(n2log n + en), gdzie n jest liczbą wierzchołków, a e jest liczbą krawędzi. Dla grafów rzadkich (ze stosunkowo małą liczbą krawędzi) jest to złożoność lepsza, niż złożoność algorytmu Floyda-Warshalla.
Algorytm Bellmana-Forda – algorytm służący do wyznaczania najkrótszych ścieżek w grafie. Wyznacza najkrótsze ścieżki z jednego wierzchołka (zwanego wierzchołkiem źródłowym) do pozostałych wierzchołków. W odróżnieniu od algorytmu Dijkstry, algorytm Bellmana-Forda dopuszcza krawędzie o ujemnych wagach, nie mogą istnieć jednak ujemne cykle osiągalne z wierzchołka źródłowego. Algorytm może być również wykorzystywany do sprawdzania, czy w grafie występują ujemne cykle.
Algorytm występuje również pod nazwą algorytm Bellmana-Forda-Moore’a.
Notacja dużego O – notacja przedstawiająca asymptotyczne tempo wzrostu, wykorzystywana do zapisywania złożoności obliczeniowej algorytmu. Za pomocą tej notacji zapisywany jest rząd wielkości funkcji wyrażającej liczbę operacji dominujących (w przypadku złożoności czasowej) lub rozmiar wymaganej pamięci (w przypadku złożoności pamięciowej) w zależności od liczby danych wejściowych.
Wykorzystując notację dużego O nie podajemy dokładnego wzoru funkcji, a jedynie jej najbardziej znaczący składnik, w dodatku z pominięciem stałego współczynnika. Przykładowo, funkcję postaci f(n)=5n2+20n+100 możemy zapisać jako O(n2). Zakładamy bowiem, że dla dostatecznie dużych n wpływ pomijanych elementów jest znikomy. Choć oczywiście dla małych n może się zdarzyć, że funkcja o gorszej złożoności będzie się wykonywała szybciej.
Weźmy dla przykładu funkcje f(n) = 1000n+2000 i g(n) = n2. Choć pierwsza funkcja ma pozornie bardzo duże stałe współczynniki, to dla n ≥ 1002 będzie ona przyjmowała wartości mniejsze. Im większe n, tym ta różnica będzie wyraźniejsza. Dla n = 10000 (w przypadku danych przetwarzanych komputerowo nie jest to wielka wartość) f(n) = 10002000 (ok. 10 mln), a g(n) = 100000000 (100 mln), czyli blisko 10 razy więcej.
Możliwe jest również wykorzystanie notacji dużego O dla funkcji wielu zmiennych. Wówczas zapis może wyglądać tak: O(v2e). Znajduje to zastosowanie np. dla algorytmów operujących na grafach, gdzie złożoność zależy zarówno od liczby wierzchołków, jak i liczby krawędzi w grafie.