Notacja dużego O
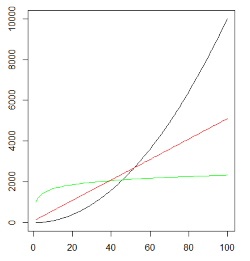(1) Wykresy funkcji: x2 (czarny), 50x+100 (czerwony) i 200log2x+1000 (zielony). Możemy zauważyć, że powyżej pewnej wartości x decydujące znaczenie ma rząd wieklości funkcji, a nie stałe współczynniki
Notacja dużego O – notacja przedstawiająca asymptotyczne tempo wzrostu, wykorzystywana do zapisywania złożoności obliczeniowej algorytmu. Za pomocą tej notacji zapisywany jest rząd wielkości funkcji wyrażającej liczbę operacji dominujących (w przypadku złożoności czasowej) lub rozmiar wymaganej pamięci (w przypadku złożoności pamięciowej) w zależności od liczby danych wejściowych.
Wykorzystując notację dużego O nie podajemy dokładnego wzoru funkcji, a jedynie jej najbardziej znaczący składnik, w dodatku z pominięciem stałego współczynnika. Przykładowo, funkcję postaci f(n)=5n2+20n+100 możemy zapisać jako O(n2). Zakładamy bowiem, że dla dostatecznie dużych n wpływ pomijanych elementów jest znikomy. Choć oczywiście dla małych n może się zdarzyć, że funkcja o gorszej złożoności będzie się wykonywała szybciej.
Weźmy dla przykładu funkcje f(n) = 1000n+2000 i g(n) = n2. Choć pierwsza funkcja ma pozornie bardzo duże stałe współczynniki, to dla n ≥ 1002 będzie ona przyjmowała wartości mniejsze. Im większe n, tym ta różnica będzie wyraźniejsza. Dla n = 10000 (w przypadku danych przetwarzanych komputerowo nie jest to wielka wartość) f(n) = 10002000 (ok. 10 mln), a g(n) = 100000000 (100 mln), czyli blisko 10 razy więcej.
Możliwe jest również wykorzystanie notacji dużego O dla funkcji wielu zmiennych. Wówczas zapis może wyglądać tak: O(v2e). Znajduje to zastosowanie np. dla algorytmów operujących na grafach, gdzie złożoność zależy zarówno od liczby wierzchołków, jak i liczby krawędzi w grafie.
Przykładowe rzędy złożoności
Przykładowe rzędy złożoności funkcji (posortowane rosnąco) to:
- O(1) – złożoność stała,
- O(logn) – złożoność logarytmiczna,
- O(n) – złożoność liniowa,
- O(nlogn) – złożoność liniowo-logarytmiczna,
- O(n2) – złożoność kwadratowa,
- O(nk), gdzie k jest stałą – złożoność wielomianowa,
- O(kn), gdzie k jest stałą – złożoność wykładnicza,
- O(n!) – złożoność rzędu silnia,
Przyjmuje się, że największą akceptowalną złożonością obliczeniową algorytmu jest złożoność wielomianowa. Istnieją jednak problemy obliczeniowe, dla których algorytm o takiej złożoności nie jest znany i być może w ogóle nie da się go opracować. Znanym przykładem takiego problemu jest problem komiwojażera.
Formalna definicja
Zapis f(n) = O(g(n)) oznacza, że istnieje taka wartość n0, że dla każdego n większego od n0 jest spełniona nierówność: f(n) ≤ cg(n), gdzie c jest stałą wartością.
W zapisie tym można zauważyć pewną nieścisłość. O(g(n)) nie jest pojedynczą funkcją, ale całym ich zbiorem. Dlatego prawidłowym zapisem powinno być f(n) ∈ O(g(n)). Powszechnie używany jest jednak zapis ze znakiem równości.
Można również zauważyć, że definicja ta stanowi tylko ograniczenie górne. W związku z tym zapisy typu 2n = O(n10) są poprawne, choć bardzo nieprecyzyjne. Podobnie, jak stwierdzenie mam w kieszeni co najwyżej kilka tysięcy złotych jest prawdziwe również wtedy, gdy mówiący ma w kieszeni złotówkę.
Notacje pokrewne
Jak już zauważyliśmy, notacja dużego O określa asymptotyczne ograniczenie górne. W analogiczny sposób można zapisać asymptotyczne ograniczenie dole. Do jego zapisu wykorzystywana jest notacja Ω (omega). Formalnie można ją zdefiniować tak: f(n) = Ω(g(n)) oznacza, że istnieje taka wartość n0, że dla każdego n większego od n0 jest spełniona nierówność: f(n) ≥ cg(n), gdzie c jest stałą wartością.
Łącząc ograniczenie górne i dolne otrzymujemy oszacowanie asymptotycznie dokładne. Do jego zapisu wykorzystywana jest notacja Θ (theta). Aby można było zapisać f(n) = Θ(g(n)), prawdziwe musi być zarówno wyrażenie f(n) = Ω(g(n)), jak i f(n) = O(g(n)).
Można z tego wysnuć wniosek, że notacja Θ jako najbardziej precyzyjna powinna być najczęściej używana. Jednak jej używanie do zapisu złożoności często byłoby błędne, gdyż nie uwzględniłoby przypadków optymistycznych. Przykładowo, pesymistyczna (a nawet średnia) złożoność czasowa sortowania przez wstawianie jest rzędu O(n2). Jeśli jednak dane są wstępnie posortowane, to złożoność redukuje się do O(n). Tak więc stwierdzenie, że algorytm ma złożoność Θ(n2) byłoby nadużyciem. Dlatego bezpieczniejsze jest stosowanie notacji dużego O.
W tym miejscu warto zauważyć, że do zapisu notacji dużego O tak naprawdę powinna być stosowana nie łacińska litera „O”, ale grecka litera „Ο” (omikron).
Bibliografia
- T.H. Cormen, Ch.E. Leiserson, R.L. Rivest, C. Stein, Wprowadzenie do algorytmów, Wydawnictwo Naukowe PWN, Warszawa, 2012, ISBN 9788301169114.
- A.Y. Bhargava, Algorytmy. Ilustrowany przewodnik, Wydawnictwo HELION, 2017, ISBN 9788328334458 [fragment książki (pdf) • książka w księgarni Helion.pl].
- R.L. Graham, D.E. Knuth, O. Patashnik, Matematyka konkretna, Wydawnictwo Naukowe PWN , Warszawa, 2012, ISBN 9788301147648 [książka w księgarni Helion.pl].
Liczba głosów: 7.
- Algorytm
- Graf
- Kolejka
- Notacja dużego O
- Rekurencja
- Stos
Dodano: 1 lutego 2018 16:17, ostatnia edycja: 2 maja 2020 16:35.
Zobacz też
Powtarzalny algorytm najbliższego sąsiada (ang. repetitive nearest neighbour algorithm, w skrócie RNN) – algorytm służący do rozwiązywania problemu komiwojażera korzystający z algorytmu najbliższego sąsiada.
Algorytm polega na wielokrotnym wykonaniu algorytmu najbliższego sąsiada w taki sposób, aby każdy wierzchołek raz był wierzchołkiem początkowym. Następnie algorytm zwraca najlepsze spośród otrzymanych rozwiązań.
Dla grafu pełnego algorytm ma złożoność O(n3), gdzie n jest liczbą wierzchołków. W trakcie wykonywania algorytmu RNN n razy zostanie wykonany algorytm najbliższego sąsiada, który ma złożoność czasową O(n2).
Algorytm RNN nie daje gwarancji znalezienia rozwiązania optymalnego. W odróżnieniu od algorytmu najbliższego sąsiada daje jednak gwarancję, że zwróci rozwiązanie co najmniej tak dobre, jak n/2-1 innych rozwiązań (dowód i więcej informacji na ten temat znajduje się w pracy podanej w bibliografii).
Rekurencja (inaczej rekursja) – odwołanie się funkcji lub definicji do samej siebie. Mówiąc inaczej, podejście rekurencyjne polega na tym, że rozwiązanie problemu wyraża się za pomocą rozwiązania tego samego problemu dla mniejszych danych wejściowych. Stosowanie rekurencji jest charakterystyczne dla algorytmów projektowanych metodą dziel i zwyciężaj.
Typowym problemem, dla którego można zastosować rekurencję, jest obliczanie silni. Przypomnijmy, że silnia z n jest zdefiniowana jako n!=1×2×…×n. Funkcja ta może być równoważnie zapisana jako:
n!=(n−1)!×n, dla n>0,
n!=1, dla n=0.
W powyższym przykładzie górny wiersz jest ogólnym równaniem rekurencji, zaś dolny wiersz jest wartością brzegową. W języku C++ powyższa funkcja byłaby zapisana w poniższy sposób.
int silnia(int n)
{
if (n > 0)
{
return n * silnia(n-1);
}
else
{
return 1;
}
};
Przekształcenie postaci rekurencyjnej funkcji do postaci zwartej (tzn. takiej, która nie zawiera odwołania do samej siebie) jest określane jako rozwiązanie rekurencji. Metody rozwiązywania rekurencji są dostępne między innymi w książkach podanych w bibliografii.
Algorytmy stosujące rekurencję są zazwyczaj proste w implementacji. Jednocześnie wiążą się one z pewnymi problemami. Przy podejściu rekurencyjnym ta sama funkcja jest wywoływana wielokrotnie, co zużywa pamięć operacyjną (w skrajnych przypadkach może to spowodować przepełnienie stosu).
Algorytm – przepis, zbiór poleceń, opis ciągu operacji prowadzących do rozwiązania konkretnego problemu. Algorytm możemy również rozumieć jako funkcję przekształcającą dane wejściowe w dane wyjściowe.
Algorytm musi być skończony, czyli jego zapis ma składać się ze skończonej liczby znaków. Musi również być poprawny, czyli dla wszystkich możliwych danych wejściowych powinien zwracać prawidłowy wynik (może być nim informacja o braku rozwiązania). Algorytm musi wykazywać również własność stopu – niezależnie od danych wejściowych obliczenia algorytmu powinny dochodzić do punktu końcowego, czyli po prostu kończyć się (nie mogą np. wpadać w nieskończoną iterację). Zapis algorytmu musi być precyzyjny, bez jakichkolwiek niejasności.