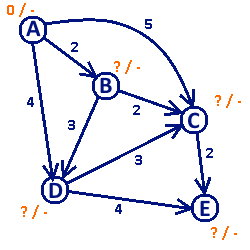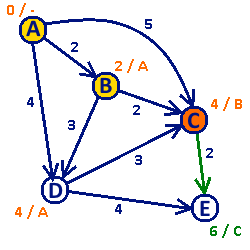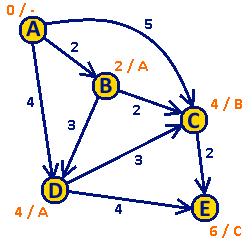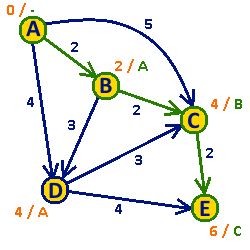
Algorytm Dijkstry

Algorytm Dijkstry – algorytm służący do wyznaczania najkrótszych ścieżek w grafie. Wyznacza najkrótsze ścieżki z jednego wierzchołka (zwanego wierzchołkiem źródłowym) do pozostałych wierzchołków. Algorytm wymaga, aby wagi krawędzi grafu nie były ujemne. Autorem algorytmu jest holenderski naukowiec Edsger Dijkstra.
Algorytm realizuje podejście zachłanne. W każdej iteracji wybierany jest ten spośród nieodwiedzonych wierzchołków, do którego można dotrzeć najmniejszym kosztem. Po wyznaczeniu ścieżki do konkretnego wierzchołka nie zostanie ona zmodyfikowana w trakcie wykonywania dalszej części algorytmu.
Opis działania algorytmu
W trakcie wykonywania algorytmu dla każdego wierzchołka zostają wyznaczone dwie wartości: koszt dotarcia do tego wierzchołka oraz poprzedni wierzchołek na ścieżce. Na początku działania algorytmu dla wierzchołka źródłowego koszt dotarcia wynosi 0 (już tam jesteśmy), a dla każdego innego wierzchołka nieskończoność (w ogóle nie wiemy, jak się tam dostać). Wszystkie wierzchołki na początku znajdują się w zbiorze Q (są to wierzchołki nieprzejrzane). Następnie algorytm przebiega następująco:
- Dopóki zbiór Q nie jest pusty:
- Pobierz ze zbioru Q wierzchołek o najmniejszym koszcie dotarcia. Oznacz go jako v i usuń ze zbioru Q.
- Dla każdej krawędzi wychodzącej z wierzchołka v (oznaczmy ją jako k) wykonaj następujące czynności:
- Oznacz wierzchołek znajdujący się na drugim końcu krawędzi k jako u.
- Jeśli koszt dotarcia do wierzchołka u z wierzchołka v poprzez krawędź k jest mniejszy od aktualnego kosztu dotarcia do wierzchołka u, to:
- Przypisz kosztowi dotarcia do wierzchołka u koszt dotarcia do wierzchołka v powiększony o wagę krawędzi k.
- Ustaw wierzchołek v jako poprzednik wierzchołka u.
Złożoność czasowa
Oznaczmy liczbę wierzchołków przez n, a liczbę krawędzi przez e. Każda krawędź będzie analizowana jeden raz w przypadku grafu skierowanego lub dwa razy w przypadku grafu nieskierowanego. Oprócz analizy krawędzi w trakcie wykonywania algorytmu n razy przeszukuje się zbiór Q. W przypadku przechowywania zbioru Q w zwykłej tablicy wyszukanie wierzchołka odbywa się w czasie liniowym (O(n)). Wówczas złożoność czasowa algorytmu to O(n2+e). Biorąc pod uwagę, że w przypadku braku krawędzi wielokrotnych liczba krawędzi jest zawsze mniejsza od n2, można powiedzieć, że złożoność czasowa algorytmu to O(n2).
Jeśli zbiór Q będziemy przechowywać w postaci kopca, wyszukiwanie elementu będzie się odbywało w czasie O(logn). Jednak po każdej zmianie kosztu dotarcia do wierzchołka trzeba przebudować kopiec, co również odbywa się w czasie O(logn). Złożoność obliczeniowa algorytmu wyniesie wówczas O(elogn). Dla grafów rzadkich (liczba krawędzi mniejsza pod względem rzędu wielkości od n2/logn) jest to zatem rozwiązanie szybsze, ale dla grafów gęstych – wolniejsze.
Jeśli do przechowywania zbioru Q zastosujemy kopiec Fibonacciego, złożoność obliczeniowa algorytmu zmniejszy się do O(nlogn+e).
Bibliografia
- T.H. Cormen, Ch.E. Leiserson, R.L. Rivest, C. Stein, Wprowadzenie do algorytmów, Wydawnictwo Naukowe PWN, Warszawa, 2012, ISBN 9788301169114.


Liczba głosów: 19.
- Algorytm Bellmana-Forda
- Algorytm Dijkstry
- Algorytm Floyda-Warshalla
- Algorytm Johnsona
Dodano: 17 marca 2017 15:07, ostatnia edycja: 26 stycznia 2019 17:49.
Zobacz też
Algorytmy zachłanne (ang. greedy algorithms) – algorytmy podejmujące w każdym kroku taką decyzję, która w danej chwili wydaje się najkorzystniejsza. Inaczej mówiąc, algorytmy zachłanne dokonują zawsze wyborów lokalnie optymalnych licząc, że doprowadzi to do znalezienia rozwiązania globalnie optymalnego. W ogólnym przypadku algorytmy zachłanne nie zawsze znajdują rozwiązanie optymalne. Są one zatem podzbiorem algorytmów heurystycznych. Jednocześnie są to algorytmy deterministyczne – nie ma w nich losowości.
Bardzo prostym przykładem algorytmu zachłannego może być szukanie najwyższego punktu na określonym obszarze poprzez przesuwanie się zawsze w kierunku największego nachylenia (nigdy się nie cofając ani nie rozpatrując kilku wariantów drogi). Jak widać, w ten sposób prawdopodobnie dojdziemy do wierzchołka położonego najbliżej od punktu początkowego, który niekoniecznie będzie najwyższym.
Metoda Forda-Fulkersona – algorytm służący do wyznaczania maksymalnego przepływu. Jest to algorytm bardzo ogólny, dlatego często nie jest nazywany algorytmem, a metodą. Popularną implementacją tej metody jest algorytm Edmondsa-Karpa. Algorytm można opisać następująco:
- Wyznacz sieć residualną (opis sieci residualnej znajduje się w dalszej części artykułu).
- Znajdź w sieci residualnej dowolną ścieżkę powiększającą.
- Jeśli nie udało się wyznaczyć żadnej ścieżki powiększającej, zakończ działanie algorytmu.
- W przeciwnym razie zwiększ przepływ w sieci (w sposób opisany w dalszej części artukułu) i wróć do punktu 1.
Zanieczyszczenie Giniego (ang. Gini Impurity) – miara niejednorodności danego zbioru wyrażająca się wzorem:
gdzie pn jest prawdopodobieństwem przynależności elementu do klasy n, czyli liczbą elementów danej klasy podzieloną przez liczbę elementów całego zbioru. Jeśli wszystkie elementy zbioru należą do tej samej klasy, zanieczyszczenie Giniego jest równe 0.
Zanieczyszczenia Giniego nie należy mylić ze współczynnikiem Giniego. Są to miary służące do wyrażania zupełnie innych rzeczy. Współczynnik Giniego określa nierównomierność rozkładu i jest wykorzystywany między innymi do liczbowego wyrażania nierówności w dochodach danego społeczeństwa.