Stos (ang. Stack) – struktura danych, w której bezpośredni dostęp jest tylko do ostatnio dodanego elementu. Stos bywa określany także jako kolejka LIFO (z ang. Last In, First Out, czyli: ostatni na wejściu, pierwszy na wyjściu). Stos można sobie wyobrazić jako kilka rzeczy ułożonych „jedna na drugiej” – łatwo można wziąć tylko rzecz leżącą na samym wierzchu, gdyż pozostałe są przykryte.

REKLAMA

Implementacja

W tej sekcji przedstawiona jest przykładowa implementacja w języku C++ stosu przechowującego liczby typu int. Opis ten jest adresowany przede wszystkim do osób, które dopiero chcą zrozumieć ideę dynamicznych struktur danych, zatem jest on dość opisowy.

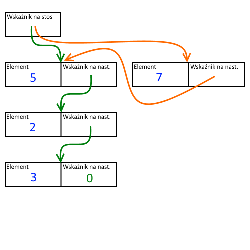
Elementem leżącym na stosie będzie nie sama liczba, ale struktura (nazwijmy ją sobie ElementStosu) zawierająca:

• Przechowywany element (w naszym przypadku będzie to liczba typu int),
• Wskaźnik do kolejnego elementu.

W kodzie programu tworzymy zmienną typu ElementStosu*, która jest wskaźnikiem na element znajdujący się na wierzchu stosu. Początkowo nasz stos jest pusty, więc wskaźnik ten ma przypisaną zerową wartość. Potrzebne nam są teraz funkcje umożliwiające dodanie elementu na stos oraz pobranie elementu ze stosu. Dodanie nowego elementu powinno przebiegać następująco:

1. Tworzymy nowy element typu ElementStosu.
2. Jako element danej struktury przypisujemy liczbę, którą chcemy dodać na stos.
3. Jako wskaźnik do następnego elementu ustawiamy wskaźnik do elementu, który aktualnie jest na wierzchu stosu.
4. Ustawiamy nasz nowy element jako wierzch stosu.

Ponieważ zmienna przechowująca początek stosu jest modyfikowana, musimy przekazać ją do funkcji przez referencję (ewentualnie przez wskaźnik). Poniższy kod źródłowy zawiera implementację struktury ElementStosu, funkcji dodającej element na stos i przykładowe wykorzystanie tej funkcji w funkcji main.

struct ElementStosu
{
	int liczba;
	ElementStosu* nastepny;
};

void dodajDoStosu(ElementStosu* &stos, int liczba)
{
	ElementStosu* nowy = new ElementStosu();
	nowy->liczba = liczba;
	nowy->nastepny = stos;
	stos = nowy;
};

int main()
{
	ElementStosu* stos = 0;
	dodajDoStosu(stos, 2);
	dodajDoStosu(stos, 5);
	return 0;
}

Zwróćmy uwagę, że po dodaniu liczby 5 tracimy bezpośredni dostęp do liczby 2 – aby się do niej dostać, musielibyśmy przejść przez kolejne wskaźniki: stos->nastepny->liczba. Zastanówmy się teraz, jak pobrać liczbę z wierzchu stosu. Tym razem musimy przestawić wskaźnik wierzchu stosu na drugi element, a pierwszy element przeczytać i usunąć. Wygląda to następująco:

1. Odczytujemy liczbę z dawnego pierwszego elementu stosu, zapisujemy ją do tymczasowej zmiennej,
2. Tworzymy tymczasowy wskaźnik do pierwszego elementu stosu,
3. Ustawiamy drugi element stosu jako jego wierzch,
4. Usuwamy z pamięci element, na który wskazuje tymczasowy wskaźnik,
5. Zwracamy liczbę odczytaną w punkcie 1.

Kod źródłowy takiej funkcji jest następujący:

int pobierzZeStosu(ElementStosu* &stos)
{
	int liczba = stos->liczba;
	ElementStosu* doUsuniecia = stos;
	stos = stos->nastepny;
	delete doUsuniecia;
	return liczba;
};

Warto zauważyć, że wywołanie tej funkcji jest możliwe tylko wtedy, gdy stos nie jest pusty – w przeciwnym razie program zakończy się błędem. Podstawowe funkcje stosu mamy już zaimplementowane. Żeby móc wygodnie przetestować ich działanie napiszmy jeszcze funkcję, która wypisze nam całą zawartość stosu. Jak wspominaliśmy, bezpośredni dostęp mamy tylko do wierzchu stosu. Żeby dostać się głębiej, musimy „przewijać” stos przechodząc po kolejnych wskaźnikach. Algorytm ten jest następujący:

1. Utwórz tymczasowy wskaźnik, początkowo niech pokazuje on na wierzch stosu,
2. Jeśli wskaźnik ma wartość 0 (jesteśmy na końcu stosu), zakończ wypisywanie. W przeciwnym razie:
3. Wypisz wartość aktualnego elementu,
4. Ustaw tymczasowy wskaźnik na kolejny element stosu,
5. Wróć do punktu 2.

Pełny przykład programu, zawierający wszystkie opisane w tym artykule funkcje, jest zamieszczony poniżej.

#include<iostream>

using namespace std;

struct ElementStosu
{
	int liczba;
	ElementStosu* nastepny;
};

void dodajDoStosu(ElementStosu* &stos, int liczba)
{
	ElementStosu* nowy = new ElementStosu();
	nowy->liczba = liczba;
	nowy->nastepny = stos;
	stos = nowy;
};

int pobierzZeStosu(ElementStosu* &stos)
{
	int liczba = stos->liczba;
	ElementStosu* doUsuniecia = stos;
	stos = stos->nastepny;
	delete doUsuniecia;
	return liczba;
};

void wypiszStos(ElementStosu* &stos)
{
	ElementStosu* aktualny = stos;
	while (aktualny != 0)
	{
		cout << aktualny->liczba << " ";
		aktualny = aktualny->nastepny;
	}
	cout << "\n";
};

int main()
{
	ElementStosu* stos = 0;
	dodajDoStosu(stos, 2);
	dodajDoStosu(stos, 5);
	dodajDoStosu(stos, 7);

	wypiszStos(stos);

	int pobrane = pobierzZeStosu(stos);
	cout << "Pobrano: " << pobrane << "\n";
	wypiszStos(stos);

	dodajDoStosu(stos, 6);
	wypiszStos(stos);

	system("pause");

	// Czyszczenie pamięci
	while (stos != 0)
	{
		pobierzZeStosu(stos);
	}

	return 0;
}

Zobacz też

• Kolejka