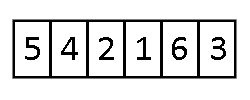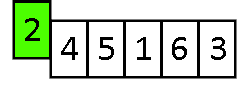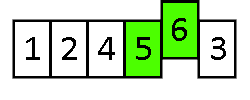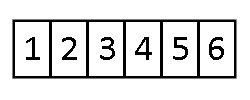Metoda przyrostowa
Metoda przyrostowa – technika projektowania algorytmów polegająca na dodawaniu do rozwiązania kolejnych elementów z danych wejściowych. Przykładem algorytmu opartego na tej metodzie jest sortowanie przez wstawianie, gdzie kolejne elementy są wstawiane do posortowanej części tablicy.
Jest to metoda prosta, jednak sprawdza się tylko dla niektórych problemów obliczeniowych.
Bibliografia
- T.H. Cormen, Ch.E. Leiserson, R.L. Rivest, C. Stein, Wprowadzenie do algorytmów, Wydawnictwo Naukowe PWN, Warszawa, 2012, ISBN 9788301169114.


Liczba głosów: 5.
- Algorytmy heurystyczne
- Dziel i zwyciężaj
- Metoda przyrostowa
- Programowanie dynamiczne
Dodano: 28 czerwca 2017 15:16, ostatnia edycja: 30 stycznia 2019 15:50.
Zobacz też
Bogosort – bardzo słaby algorytm sortowania oparty na metodzie prób i błędów. Polega na ustawianiu elementów w losowej kolejności i sprawdzaniu, czy są posortowane. Średnia złożoność tego algorytmu jest rzędu silnia, a w przypadku pesymistycznym algorytm będzie działał w nieskończoność.
Algorytm występuje też w nieco ulepszonej wersji, w której nie sprawdza się wielokrotnie tego samego ustawienia. Wówczas algorytm daje gwarancję znalezienia rozwiązania, jednak jego złożoność czasowa nadal jest rzędu silnia (w przypadku pesymistycznym trzeba sprawdzić wszystkie permutacje zbioru).
Ze względu na bardzo dużą złożoność czasową bogosort nie nadaje się do praktycznych zastosowań. Istnieją proste w implementacji, a znacznie wydajniejsze algorytmy sortujące, np. sortowanie przez wstawianie.
Notacja dużego O – notacja przedstawiająca asymptotyczne tempo wzrostu, wykorzystywana do zapisywania złożoności obliczeniowej algorytmu. Za pomocą tej notacji zapisywany jest rząd wielkości funkcji wyrażającej liczbę operacji dominujących (w przypadku złożoności czasowej) lub rozmiar wymaganej pamięci (w przypadku złożoności pamięciowej) w zależności od liczby danych wejściowych.
Wykorzystując notację dużego O nie podajemy dokładnego wzoru funkcji, a jedynie jej najbardziej znaczący składnik, w dodatku z pominięciem stałego współczynnika. Przykładowo, funkcję postaci f(n)=5n2+20n+100 możemy zapisać jako O(n2). Zakładamy bowiem, że dla dostatecznie dużych n wpływ pomijanych elementów jest znikomy. Choć oczywiście dla małych n może się zdarzyć, że funkcja o gorszej złożoności będzie się wykonywała szybciej.
Weźmy dla przykładu funkcje f(n) = 1000n+2000 i g(n) = n2. Choć pierwsza funkcja ma pozornie bardzo duże stałe współczynniki, to dla n ≥ 1002 będzie ona przyjmowała wartości mniejsze. Im większe n, tym ta różnica będzie wyraźniejsza. Dla n = 10000 (w przypadku danych przetwarzanych komputerowo nie jest to wielka wartość) f(n) = 10002000 (ok. 10 mln), a g(n) = 100000000 (100 mln), czyli blisko 10 razy więcej.
Możliwe jest również wykorzystanie notacji dużego O dla funkcji wielu zmiennych. Wówczas zapis może wyglądać tak: O(v2e). Znajduje to zastosowanie np. dla algorytmów operujących na grafach, gdzie złożoność zależy zarówno od liczby wierzchołków, jak i liczby krawędzi w grafie.
Ten artykuł opisuje algorytm zachłanny rozwiązujący problem wydawania reszty. Algorytm ten polega na wybieraniu zawsze największej dostępnej monety, tzn. takiej, która nie jest większa od kwoty pozostałej do wydania.
Algorytm nie zawsze znajduje rozwiązanie optymalne. Przykładowo, dla zbioru nominałów {1, 3, 4} i kwoty 6 algorytm użyje najpierw monety o nominale 4 (pozostaje do wydania kwota 2), potem monety o nominale 1 (pozostaje kwota 1) i jeszcze raz monety o nominale 1. Łącznie algorytm użyje więc trzech monet, podczas gdy rozwiązanie optymalne wymaga użycia tylko dwóch (dwie monety o nominale 3).