Przeszukiwanie w głąb
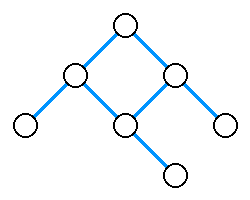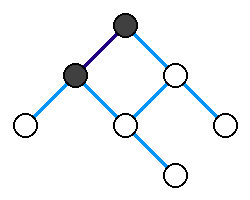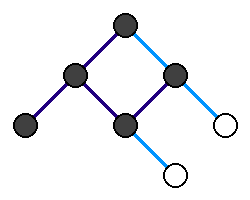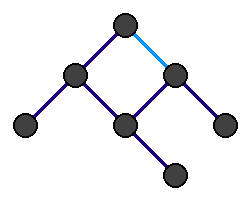
Przeszukiwanie w głąb (ang. depth-first search, w skrócie DFS) – jeden z dwóch podstawowych algorytmów przeszukiwania grafu. Polega na przechodzeniu zawsze do kolejnego nieodwiedzonego wierzchołka. Jeśli dany wierzchołek nie ma nieodwiedzonych sąsiadów, wracamy do poprzedniego wierzchołka i sprawdzamy jego sąsiadów. Mówiąc obrazowo, w algorytmie tym wchodzimy tak głęboko, jak to możliwe (przechodzimy dalej, dopóki się da).
Algorytm można zapisać w sposób rekurencyjny. Wywoływana rekurencyjnie procedura działa następująco: oznacz wierzchołek jako odwiedzony, a następnie wywołaj tę procedurę dla każdego sąsiada danego wierzchołka, jeśli nie został on wcześniej odwiedzony. Na początku wywołujemy procedurę dla wierzchołka początkowego.
Złożoność
Złożoność algorytmu jest rzędu O(v+e) – musimy sprawdzić wszystkie krawędzie i oznaczyć wszystkie wierzchołki. Jeśli każdy wierzchołek jest osiągalny ze źródła (po zakończeniu działania algorytmu nie będzie nieodwiedzonych wierzchołków), to e ≥ (v−1). Przy takim założeniu złożoność czasowa algorytmu wynosi O(e).
Liczba głosów: 5.
- Przeszukiwanie w głąb
- Przeszukiwanie wszerz
Dodano: 27 listopada 2017 19:10, ostatnia edycja: 31 stycznia 2018 16:19.
Zobacz też
Dziel i zwyciężaj (ang. divide and conquer) – technika projektowania algorytmów polegająca na podejściu rekurencyjnym. W technice tej problem dzielony jest na mniejsze podproblemy, te podproblemy na jeszcze mniejsze podproblemy, aż dojdzie się do przypadków trywialnych (np. posortowanie jednoelementowej tablicy, obliczenie silni z 1).
Jeśli rozpatrywany problem wymaga podzielenia na podproblemy, jest on określany jako przypadek rekurencyjny. Jeśli mamy do czynienia z przypadkiem trywialnym, jest to przypadek bazowy. Tworząc algorytm wykorzystujący metodę dziel i zwyciężaj musimy ustalić:
- Jak rozwiązać przypadek bazowy (trywialny).
- Jak wyznaczyć rozwiązanie problemu, mając dostępne rozwiązania podproblemów.
Przykładem algorytmu opartego na tej metodzie jest sortowanie przez scalanie.
Metoda Forda-Fulkersona – algorytm służący do wyznaczania maksymalnego przepływu. Jest to algorytm bardzo ogólny, dlatego często nie jest nazywany algorytmem, a metodą. Popularną implementacją tej metody jest algorytm Edmondsa-Karpa. Algorytm można opisać następująco:
- Wyznacz sieć residualną (opis sieci residualnej znajduje się w dalszej części artykułu).
- Znajdź w sieci residualnej dowolną ścieżkę powiększającą.
- Jeśli nie udało się wyznaczyć żadnej ścieżki powiększającej, zakończ działanie algorytmu.
- W przeciwnym razie zwiększ przepływ w sieci (w sposób opisany w dalszej części artukułu) i wróć do punktu 1.