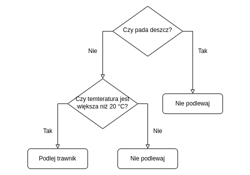
Drzewo decyzyjne
Drzewo decyzyjne – metoda graficzna wspierająca podejmowanie decyzji, jak również model stosowany w uczeniu maszynowym do klasyfikacji lub regresji.
Podejmowanie decyzji z wykorzystaniem drzewa decyzyjnego odbywa się poprzez odpowiadanie na kolejne pytania. Pojedyncze pytanie musi być proste i dotyczyć jednego konkretnego atrybutu. Pytania ułożone są w strukturę hierarchiczną – wybór następnego pytania (lub końcowej decyzji) zależy od odpowiedzi udzielonej na poprzednie.
Proste drzewo decyzyjne może być w pełni zaprojektowane już przy tworzeniu programu i zaimplementowane w kodzie np. za pomocą instrukcji warunkowych. W uczeniu maszynowym drzewo jest generowane automatycznie na podstawie próbek ze zbioru uczącego.
Teoria grafów
Drzewo to taki graf, który jest:
- prosty – wybraną parę wierzchołków może bezpośrednio łączyć co najwyżej jedna krawędź,
- spójny – między dowolną parą wierzchołków da się wyznaczyć ścieżkę,
- acykliczny – taka ścieżka jest dokładnie jedna.
W drzewie decyzyjnym poszczególne węzły (wierzchołki, z których wychodzą co najmniej dwie krawędzie) zawierają proste kryteria podziału, np. sprawdzanie, czy wartość danego atrybutu jest większa od pewnej wartości. Proces decyzyjny rozpoczyna się od węzła określanego jako korzeń. Następnie, w zależności od rezultatu sprawdzania danego kryterium, przechodzi się do kolejnych węzłów. Liście (wierzchołki mające tylko jednego sąsiada) oznaczają końcowe decyzje.
Uczenie maszynowe
Jeśli drzewo ma przewidywać klasę, do której przynależy dany obiekt, jest to drzewo klasyfikacyjne. Jeśli przewidywana jest wartość liczbowa, jest to drzewo regresyjne. Drzewa klasyfikacyjne i regresyjne zbiorczo określane są skrótowcem CART, od ang. Classification and Regression Tree.
Drzewo w uczeniu maszynowym tworzone jest automatycznie na podstawie próbek ze zbioru uczącego. Algorytmy tworzenia drzewa decyzyjnego mogą być różne, polegają one na dodawaniu kolejnych węzłów w taki sposób, aby zbiory próbek mieszczących się w obrębie jednego liścia były jak najbardziej jednorodne. Typowy algorytm budowy drzewa decyzyjnego można zapisać następująco:
- Wybierz taki podział zbioru (przez podział rozumiemy atrybut i próg), żeby dwa powstałe w ten sposób podzbiory były jak najbardziej jednorodne. W przypadku drzew klasyfikacyjnych do oceny niejednorodności zbioru często wykorzystywany jest wskaźnik zanieczyszczenia Giniego, w przypadku drzew regresyjnych – odchylenie standardowe.
- Dla każdego z otrzymanych podzbiorów:
- Jeśli spełniony jest warunek stopu (osiągnięta wystarczająco niska niejednorodność zbioru lub maksymalna głębokość drzewa), utwórz w tym miejscu liść. W przypadku klasyfikacji wartością tego liścia jest ta klasa, która występuje w otrzymanym zbiorze najczęściej. W przypadku regresji zwracaną wartością jest średnia elementów.
- W przeciwnym razie wróć do punku 1.
Aby uniknąć przeuczenia, czasami stosuje się dodatkowo mechanizm przycinania (ang. prunning) polegający na tym, żeby usunąć część gałęzi.
Bibliografia
- P. Gupta, Decision Trees in Machine Learning, Towards Data Science, 2017 [Dostęp 2022-09-17].
- J. Kozak, P. Juszczuk , Algorytmy do konstruowania drzew decyzyjnych w przewidywaniu skuteczności kampanii telemarketingowej banku, Studia Informatica Pomerania, nr 39 , 2016, s. 49-59, DOI: 10.18276/si.2016.39-05.
Liczba głosów: 0.
- Drzewo decyzyjne
- Matroid
- Zanieczyczczenie Giniego
Dodano: 17 września 2022 18:46, ostatnia edycja: 20 września 2022 19:03.
Zobacz też
Metoda przyrostowa – technika projektowania algorytmów polegająca na dodawaniu do rozwiązania kolejnych elementów z danych wejściowych. Przykładem algorytmu opartego na tej metodzie jest sortowanie przez wstawianie, gdzie kolejne elementy są wstawiane do posortowanej części tablicy.
Jest to metoda prosta, jednak sprawdza się tylko dla niektórych problemów obliczeniowych.
Problem wydawania reszty (ang. change-making problem) – problem obliczeniowy polegający na tym, aby mając określony zbiór nominałów wyrazić daną kwotę za pomocą jak najmniejszej liczby monet. Jest to szczególny przypadek problemu plecakowego.
Programowanie dynamiczne – technika projektowania algorytmów polegająca na rozwiązywaniu podproblemów i zapamiętywaniu ich wyników. W technice tej, podobnie jak w metodzie dziel i zwyciężaj, problem dzielony jest na mniejsze podproblemy. Wyniki rozwiązywania podproblemów są jednak zapisywane w tabeli, dzięki czemu w przypadku natrafienia na ten sam podproblem nie trzeba go ponownie rozwiązywać.
Wykorzystując programowanie dynamiczne można zastosować metodę zstępującą z zapamiętywaniem lub metodę wstępującą.
- Metoda zstępująca z zapamiętywaniem polega na rekurencyjnym wywoływaniu funkcji z zapamiętywaniem wyników. Metoda ta jest podobna do metody dziel i zwyciężaj – różni się od niej tym, że jeśli rozwiązanie danego problemu jest już w tabeli z wynikami, to należy je po prostu stamtąd odczytać.
- Metoda wstępująca polega na rozwiązywaniu wszystkich możliwych podproblemów, zaczynając od tych o najmniejszym rozmiarze. Wówczas w momencie rozwiązywania podproblemu na pewno są już dostępne rozwiązania jego podproblemów. W tym podejściu nie zużywa się pamięci na rekurencyjne wywołania funkcji. Może się jednak okazać, że część podproblemów została rozwiązana nadmiarowo (nie były one potrzebne do rozwiązania głównego problemu).