Algorytm Kruskala
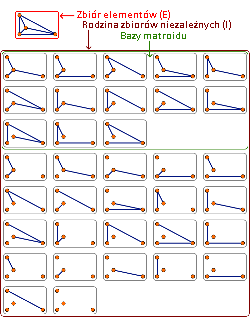(2) Reprezentacja problemu minimalnego drzewa rozpinającego za pomocą matroidu (kliknij ilustrację, aby powiększyć)
Algorytm Kruskala – algorytm wyznaczający minimalne drzewo rozpinające. Algorytm ten wykorzystuje strategię zachłanną, zawsze zwraca rozwiązanie optymalne.
Działanie algorytmu
Algorytm polega na dołączaniu do rozwiązania kolejno najkrótszych możliwych krawędzi, aż do otrzymania drzewa rozpinającego. Algorytm ten można bardziej formalnie zapisać następująco:
- Posortuj krawędzie rosnąco według ich wag, umieść je w kolejce.
- Pobierz z kolejki krawędź o najmniejszej wadze, usuń ją z kolejki.
- Jeśli wierzchołki łączone przez tę krawędź należą do różnych drzew (wówczas dołączenie krawędzi nie spowoduje utworzenia cyklu), dołącz krawędź do rozwiązania.
- Jeśli liczba krawędzi dołączonych do rozwiązania wynosi v-1 (v jest liczbą wierzchołków), zakończ działanie algorytmu. W przeciwnym razie przejdź do punktu 2.
Główna pętla algorytmu wykona się maksymalnie e razy (e jest liczbą krawędzi). W trakcie każdego przebiegu pętli trzeba jednak sprawdzić, czy daną krawędź można dołączyć do rozwiązania. Złożoność obliczeniowa algorytmu zależy od sposobu implementacji sprawdzania tego warunku, a także od sposobu sortowania kolejki krawędzi.
Aby sprawdzać, czy wierzchołki należą do różnych drzew, możemy wykorzystać zbiory wierzchołków. Na początku każdy wierzchołek będzie w osobnym zbiorze. Za każdym razem przed dołączeniem krawędzi sprawdzamy, czy wierzchołki znajdują się w różnych zbiorach. Jeśli tak, krawędź dołączamy do rozwiązania, a te dwa zbiory scalamy.
Zwracanie rozwiązań optymalnych
Algorytm Kruskala (pomimo, że jako algorytm zachłanny zalicza się do heurystyk) zawsze zwraca rozwiązanie optymalne. Problem wyznaczania minimalnego drzewa rozpinającego można przedstawić za pomocą matroidu – przykład jest pokazany na rysunku (2). Udowodniono, że w takim przypadku podejście zachłanne daje gwarancję znalezienia rozwiązania optymalnego. Pełen dowód jest dostępny w książce [1].
Bibliografia
- T.H. Cormen, Ch.E. Leiserson, R.L. Rivest, C. Stein, Wprowadzenie do algorytmów, Wydawnictwo Naukowe PWN, Warszawa, 2012, ISBN 9788301169114.
Liczba głosów: 1.
- Algorytm Kruskala
Dodano: 5 kwietnia 2017 12:16, ostatnia edycja: 24 kwietnia 2020 19:28.
Zobacz też
Algorytm Helda-Karpa (czasami określany jako algorytm Bellmana-Helda-Karpa) – algorytm służący do rozwiązywania problemu komiwojażera. Jest to algorytm dokładny oparty na programowaniu dynamicznym. Algorytm ma złożoność czasową O(n22n) i złożoność pamięciową O(n2n). Jest to co prawda złożoność gorsza od wielomianowej, ale algorytm ten jest znacznie lepszy od algorytmu sprawdzającego wszystkie warianty (złożoność czasowa O(n!)).
Ten artykuł opisuje algorytm zachłanny rozwiązujący problem wydawania reszty. Algorytm ten polega na wybieraniu zawsze największej dostępnej monety, tzn. takiej, która nie jest większa od kwoty pozostałej do wydania.
Algorytm nie zawsze znajduje rozwiązanie optymalne. Przykładowo, dla zbioru nominałów {1, 3, 4} i kwoty 6 algorytm użyje najpierw monety o nominale 4 (pozostaje do wydania kwota 2), potem monety o nominale 1 (pozostaje kwota 1) i jeszcze raz monety o nominale 1. Łącznie algorytm użyje więc trzech monet, podczas gdy rozwiązanie optymalne wymaga użycia tylko dwóch (dwie monety o nominale 3).
Metoda przyrostowa – technika projektowania algorytmów polegająca na dodawaniu do rozwiązania kolejnych elementów z danych wejściowych. Przykładem algorytmu opartego na tej metodzie jest sortowanie przez wstawianie, gdzie kolejne elementy są wstawiane do posortowanej części tablicy.
Jest to metoda prosta, jednak sprawdza się tylko dla niektórych problemów obliczeniowych.