Matroid
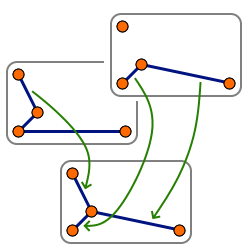(1) Własność wymiany: biorąc dwa zbiory niezależne o różnej liczbie elementów jesteśmy w stanie dodać do mniejszego z nich taki element z większego, że otrzymany zbiór także będzie należał do rodziny zbiorów niezależnych. W tym przypadku zbiorami niezależnymi są lasy rozpinające
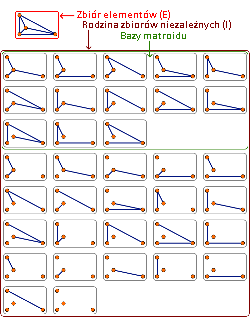(2) Reprezentacja problemu minimalnego drzewa rozpinającego za pomocą matroidu (kliknij ilustrację, aby powiększyć)
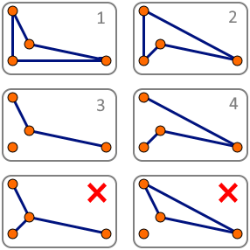(3) Przykład niespełnionej własności wymiany przy próbie przedstawiania problemu komiwojażera za pomocą matroidu. Zbiory 3 i 4 są podzbiorami poprawnych rozwiązań, więc musiałyby być zbiorami niezależnymi. Nie da się jednak do zbioru 3 dodać elementu zbioru 4 w taki sposób, aby uzyskać inny zbiór niezależny
Matroid – struktura matematyczna składająca się z niepustego zbioru elementów E i takiej rodziny jego podzbiorów I, że spełnione są następujące warunki:
- Jeśli jakiś zbiór należy do I, to wszystkie jego podzbiory także należą do I.
- Jeśli weźmiemy dowolne dwa zbiory należące do I o różnej liczbie elementów, to jesteśmy w stanie dodać do mniejszego z nich taki element z większego (spośród tych, które nie należą do mniejszego), że utworzony w ten sposób zbiór także będzie należał do I.
Drugi warunek, zwany własnością wymiany, formalnie może być zapisany jako:
$$⋀↙{A,B∊I}↙{ |A|>|B| }⋁↙{t∊(A-B)} B∪\{t\} ∈ I$$Co istotne, rodzina zbiorów I nie musi zawierać wszystkich możliwych podzbiorów zbioru E. Ważne tylko, aby była spełniona własność wymiany. Przykładowo, dla E={a,b,c,d} prawidłową rodziną I, może być zarówno { {a,b}, {b,c}, {a}, {b}, {c}, ∅}, jak i { {a}, {b}, {c}, {d}, ∅}. Trywialnym przypadkiem poprawnego matroidu jest taki, w którym rodzina I zawiera jedynie zbiór pusty.
Wybrane pojęcia
Zbiory należące do I określane są jako zbiory niezależne. Zbiór niezależny o największej liczbie elementów to baza matroidu. Matroid może mieć wiele baz. W pierwszym wspomnianym wcześniej przykładzie bazami są zbiory {a,b} i {b,c}, w drugim zaś zbiory {a}, {b}, {c}, {d}.
Jeśli każdy element zbioru E ma przyporządkowaną dodatnią liczbę (wagę), to taki matroid jest określany jako matroid ważony. Każdemu zbiorowi niezależnemu również można wtedy przyporządkować wagę, będącą sumą wag wszystkich należących do niego elementów. Dla matroidów grafowych (tzn. takich, w których elementy zbioru E są krawędziami grafu), wagą może być długość krawędzi.
Więcej pojęć związanych z matroidami można znaleźć w książce [1].
Matroidy a algorytmy zachłanne
Matroidy ważone mają duże zastosowanie przy ocenie skuteczności algorytmów zachłannych. Udowodniono, że jeśli problem obliczeniowy da się przedstawić za pomocą matroidu ważonego, to algorytm zachłanny zawsze zwróci rozwiązanie optymalne (dowód jest dostępny w książce [2]). W takim przypadku, jeśli do naszego rozwiązania będziemy zawsze dodawać ten spośród dostępnych elementów zbioru E, który ma największą wagę, to otrzymamy bazę matroidu o największej wadze spośród wszystkich baz. Przykładem takiego algorytmu jest algorytm Kruskala.
Bibliografia
- R.J. Wilson, Wprowadzenie do teorii grafów, Wydawnictwo Naukowe PWN, Warszawa, 2012, ISBN 9788301150662.
- T.H. Cormen, Ch.E. Leiserson, R.L. Rivest, C. Stein, Wprowadzenie do algorytmów, Wydawnictwo Naukowe PWN, Warszawa, 2012, ISBN 9788301169114.
Liczba głosów: 0.
Dodano: 24 kwietnia 2020 13:50, ostatnia edycja: 24 kwietnia 2020 18:28.
Zobacz też
Kolejka (ang. Queue) – struktura danych, w której elementy pobierane są z początku, a dodawane na końcu. Z kolejki można zatem pobrać tylko ten element, który był dodany najwcześniej. Kolejka bywa określana również jako kolejka FIFO (z ang. First In, First Out), w odróżnieniu od kolejki LIFO, czyli stosu.
Ten artykuł opisuje pewną modyfikację algorytmu opartego na programowaniu dynamicznym rozwiązującego problem wydawania reszty. Algorytm ten daje gwarancję znalezienia rozwiązania optymalnego. Algorytm zaproponował J.W. Wright w pracy The Change-Making Problem (link w bibliografii).
Sortowanie przez wstawianie (ang. insertion sort) – prosty algorytm sortowania polegający na wstawianiu kolejnych elementów ciągu we właściwe miejsca. Złożoności czasowa algorytmu wynosi O(n2). Jest to algorytm realizujący metodę przyrostową.