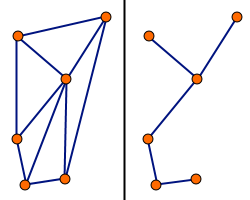
Minimalne drzewo rozpinające
Minimalne drzewo rozpinające (ang. minimum spanning tree, w skrócie MST), inaczej drzewo rozpinające o minimalnej wadze – drzewo łączące wszystkie wierzchołki pewnego grafu spójnego mające najmniejszą możliwą sumę wag krawędzi.
Jeśli graf ma v wierzchołków, to jego drzewo rozpinające zawsze będzie miało v-1 krawędzi. Jeśli ten graf ma e krawędzi, aby utworzyć drzewo rozpinające, trzeba usunąć z grafu e-v+1 krawędzi. Liczba ta jest określana jako liczba cyklomatryczna.
Wyznaczanie minimalnego drzewa rozpinającego
Minimalne drzewo rozpinające można wyznaczyć stosując algorytm Kruskala wykorzystujący strategię zachłanną. Algorytm ten polega na dołączaniu do rozwiązania kolejno najkrótszych możliwych krawędzi, aż do otrzymania drzewa rozpinającego. Przebieg algorytmu można zapisać następująco:
- Posortuj krawędzie rosnąco według ich wag, umieść je w kolejce.
- Pobierz z kolejki krawędź o najmniejszej wadze, usuń ją z kolejki.
- Jeśli wierzchołki łączone przez tę krawędź należą do różnych drzew (wówczas dołączenie krawędzi nie spowoduje utworzenia cyklu), dołącz krawędź do rozwiązania.
- Jeśli liczba krawędzi dołączonych do rozwiązania wynosi v-1 (v jest liczbą wierzchołków), zakończ działanie algorytmu. W przeciwnym razie przejdź do punktu 2.
Bibliografia
- T.H. Cormen, Ch.E. Leiserson, R.L. Rivest, C. Stein, Wprowadzenie do algorytmów, Wydawnictwo Naukowe PWN, Warszawa, 2012, ISBN 9788301169114.
Liczba głosów: 12.
Dodano: 18 października 2016 18:30, ostatnia edycja: 30 stycznia 2019 14:10.
Zobacz też
Problem komiwojażera (ang. travelling salesman problem, w skrócie TSP) – problem obliczeniowy polegający na poszukiwaniu w grafie takiego cyklu, który zawiera wszystkie wierzchołki (każdy dokładnie raz) i ma jak najmniejszy koszt. Bardziej formalnie, problem komiwojażera polega na poszukiwaniu w grafie cyklu Hammiltona o najmniejszej wadze.
Problem ma liczne zastosowania w życiu codziennym. Najlepszym przykładem jest praca kuriera, który musi wyjechać z magazynu, zawieźć przesyłki w różne miejsca i wrócić do magazynu.
Nie jest znany efektywny (tj. działający w czasie co najwyżej wielomianowym) algorytm dający gwarancję znalezienia optymalnego rozwiązania problemu komiwojażera. Problem ten jest bowiem zaliczany do klasy problemów NP-trudnych. W wersji decyzyjnej (czy istnieje cykl o długości mniejszej od x) problem jest zaliczany do klasy problemów NP-zupełnych. W grafie pełnym mającym n wierzchołków liczba możliwych cykli Hammiltona wynosi aż (n-1)!/2. W praktyce sprawdzenie wszystkich możliwości jest zatem wykonalne tylko dla niewielkiej liczby wierzchołków.
Wyznaczanie najkrótszej ścieżki – zagadnienie polegające na wyszkaniu w grafie takiej ścieżki łączącej dwa wierzchołki, której suma wag krawędzi jest jak najmniejsza.
W przypadku pesymistycznym do wyznaczenia optymalnej ścieżki z wierzchołka A do wierzchołka B konieczne jest wyznaczenie najkrótszych ścieżek z wierzchołka A do wszystkich pozostałych wierzchołków w grafie. Zagadnienie takie jest określane jako poszukiwanie najkrótszych ścieżek z jednego źródła. Do rozwiązywania tego zagadnienia można wykorzystać następujące algorytmy:
Nieco innym zagadnieniem jest poszukiwanie najkrótszych ścieżek pomiędzy każdą parą wierzchołków. W tym celu można wykorzystać algorytmy wymienione powyżej (wykonując je wielokrotnie, za każdym razem przyjmując inny wierzchołek źródłowy) lub algorytmy poszukujące od razu wszystkich ścieżek, takie jak:
Aby znalezienie najkrótszej ścieżki było możliwe, graf nie może zawierać ujemnych cykli osiągalnych z wierzchołka źródłowego. Jeśli taki cykl istnieje, to poruszając się nim „w kółko” cały czas zmniejszamy długość ścieżki. Dopuszczalne jest natomiast występowanie krawędzi o ujemnej wadze, choć nie wszystkie algorytmy dopuszczają ten przypadek.
Jeśli poszukujemy ścieżek o najmniejszej liczbie krawędzi (np. wtedy, gdy wszystkie krawędzie mają taką samą, dodatnią wagę), to zamiast powyższych algorytmów możemy skorzystać z prostego przeszukiwania grafu wszerz.
Metoda z zastosowaniem przepływu blokującego – algorytm wyznaczający maksymalny przepływ w sieci przepływowej. W algorytmie tym przepływ zwiększany jest iteracyjnie, w każdej iteracji wyznaczony przepływ jest powiększany o przepływ blokujący w warstwowej sieci residualnej.