Metoda Forda-Fulkersona
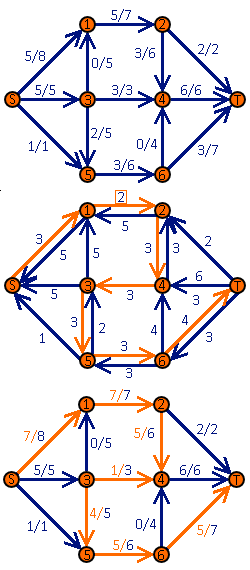(1) Sieć przepływowa z pewnym przepływem (na górze), odpowiadająca jej sieć residualna (w środku) z zaznaczoną ścieżką powiększającą i ta sama sieć przepływowa po zwiększeniu przepływu (na dole)
Metoda Forda-Fulkersona – algorytm służący do wyznaczania maksymalnego przepływu. Jest to algorytm bardzo ogólny, dlatego często nie jest nazywany algorytmem, a metodą. Popularną implementacją tej metody jest algorytm Edmondsa-Karpa. Algorytm można opisać następująco:
- Wyznacz sieć residualną (opis sieci residualnej znajduje się w dalszej części artykułu).
- Znajdź w sieci residualnej dowolną ścieżkę powiększającą.
- Jeśli nie udało się wyznaczyć żadnej ścieżki powiększającej, zakończ działanie algorytmu.
- W przeciwnym razie zwiększ przepływ w sieci (w sposób opisany w dalszej części artukułu) i wróć do punktu 1.
Sieć residualna i ścieżka powiększająca
Sieć residualna jest grafem skierowanym tworzonym na podstawie sieci przepływowej i jej aktualnego przepływu. Wagi łuków w sieci residualnej oznaczają, o ile można zmienić przepływ w odpowiadającym mu łuku sieci przepływowej.
Liczba i układ łuków w sieci residualnej mogą być nieco inne, niż w sieci przepływowej. Jeśli przepływ w danym łuku sieci przepływowej jest większy od zera, to przepływ w tym łuku da się zmniejszyć – w sieci residualnej pojawi się wówczas dodatkowo łuk skierowany w przeciwną stronę, niż łuk w sieci przepływowej. Jeśli natomiast przepływ w łuku sieci przepływowej jest już maksymalny, to nie można go zwiększyć, zatem taki łuk nie będzie występował w sieci residualnej (będzie występował tylko łuk o przeciwnym zwrocie).
Ścieżka powiększająca to ścieżka w sieci residualnej prowadząca od źródła do ujścia. Najmniejsza spośród wag łuków należących do ścieżki powiekszającej jest określana jako jej przepustowość residualna. Jest to wartość, o którą można zwiększyć przepływ w sieci przepływowej.
Powiększenie przepływu w sieci o ścieżkę powiększającą można opisać następująco. Dla każdego łuku należącego do ścieżki powiększającej:
- Jeśli taki łuk istnieje w sieci przepływowej, zwiększ jego przepływ o przepustowość residualną ścieżki powiększającej.
- Jeśli taki łuk nie istnieje w sieci przepływowej, zmniejsz przepływ w łuku o przeciwnym zwrocie o przepustowość residualną ścieżki powiększającej.
Złożoność obliczeniowa
Ze względu na to, że metoda Forda-Fulkersona jest algorytmem bardzo ogólnym, złożoność obliczeniowa zależy od konkretnej implementacji. Jeśli założymy, że przepływy w łukach są liczbami naturalnymi, to możemy oszacować górne ograniczenie tej złożoności. W każdej iteracji algorytmu powiększymy przepływ o co najmniej 1, zatem liczba wykonań głównej pętli algorytmu będzie mniejsza bądź równa od maksymalnego przepływu (oznaczmy go f). W trakcie wyznaczania ścieżki powiększającej i zwiększania przepływu musimy przejrzeć w najgorszym wypadku wszystkie krawędzie (oznaczmy ich liczbę jako e). Kres górny złożoności czasowej jest zatem rzędu O(fe).
Bibliografia
- T.H. Cormen, Ch.E. Leiserson, R.L. Rivest, C. Stein, Wprowadzenie do algorytmów, Wydawnictwo Naukowe PWN, Warszawa, 2012, ISBN 9788301169114.
- A. Debudaj-Grabysz, S. Deorowicz, J. Widuch, Algorytmy i struktury danych. Wybór zaawansowanych metod, Wydawnictwo Politechniki Śląskiej, Gliwice, 2012, ISBN 9788373359383.
Liczba głosów: 0.
- Algorytm Edmondsa-Karpa
- Metoda Forda-Fulkersona
- Metoda z zastosowaniem przepływu blokującego
Dodano: 12 grudnia 2017 15:56, ostatnia edycja: 24 kwietnia 2020 20:19.
Zobacz też
Algorytm Bellmana-Forda – algorytm służący do wyznaczania najkrótszych ścieżek w grafie. Wyznacza najkrótsze ścieżki z jednego wierzchołka (zwanego wierzchołkiem źródłowym) do pozostałych wierzchołków. W odróżnieniu od algorytmu Dijkstry, algorytm Bellmana-Forda dopuszcza krawędzie o ujemnych wagach, nie mogą istnieć jednak ujemne cykle osiągalne z wierzchołka źródłowego. Algorytm może być również wykorzystywany do sprawdzania, czy w grafie występują ujemne cykle.
Algorytm występuje również pod nazwą algorytm Bellmana-Forda-Moore’a.
Sortowanie przez scalanie – rekurencyjny algorytm sortowania wykorzystujący metodę dziel i zwyciężaj.
Programowanie dynamiczne – technika projektowania algorytmów polegająca na rozwiązywaniu podproblemów i zapamiętywaniu ich wyników. W technice tej, podobnie jak w metodzie dziel i zwyciężaj, problem dzielony jest na mniejsze podproblemy. Wyniki rozwiązywania podproblemów są jednak zapisywane w tabeli, dzięki czemu w przypadku natrafienia na ten sam podproblem nie trzeba go ponownie rozwiązywać.
Wykorzystując programowanie dynamiczne można zastosować metodę zstępującą z zapamiętywaniem lub metodę wstępującą.
- Metoda zstępująca z zapamiętywaniem polega na rekurencyjnym wywoływaniu funkcji z zapamiętywaniem wyników. Metoda ta jest podobna do metody dziel i zwyciężaj – różni się od niej tym, że jeśli rozwiązanie danego problemu jest już w tabeli z wynikami, to należy je po prostu stamtąd odczytać.
- Metoda wstępująca polega na rozwiązywaniu wszystkich możliwych podproblemów, zaczynając od tych o najmniejszym rozmiarze. Wówczas w momencie rozwiązywania podproblemu na pewno są już dostępne rozwiązania jego podproblemów. W tym podejściu nie zużywa się pamięci na rekurencyjne wywołania funkcji. Może się jednak okazać, że część podproblemów została rozwiązana nadmiarowo (nie były one potrzebne do rozwiązania głównego problemu).