Algorytm Edmondsa-Karpa
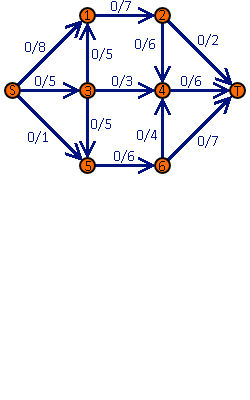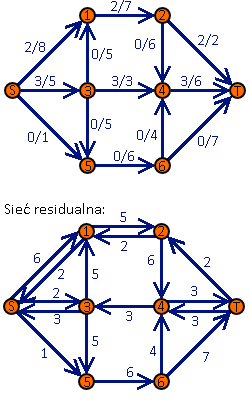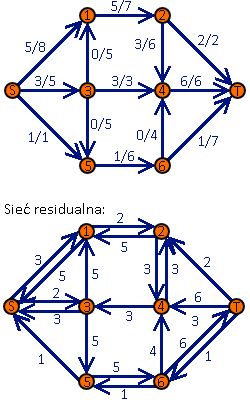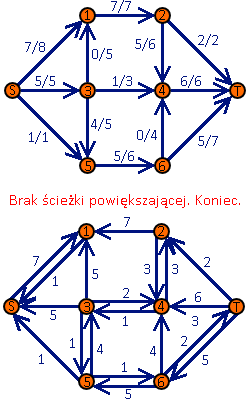(1) Animacja pokazująca przykładowe wykonanie algorytmu. W sieci przepływowej wartość przed ukośnikiem oznacza aktualny przepływ, a wartość po ukośniku – przepływ maksymalny. Ścieżka powiększająca oznaczana jest na pomarańczowo
Algorytm Edmondsa-Karpa – algorytm wyszukiwania maksymalnego przepływu w sieci przepływowej. Jest to przypadek szczególny algorytmu Forda-Fulkersona.
W algorytmie Edmondsa-Karpa ścieżka powiększająca wyznaczana jest za pomocą przeszukiwania grafu wszerz. Dzięki temu w każdej iteracji algorytmu dołączana jest zawsze najkrótsza (pod względem liczby krawędzi) ścieżka powiększająca. W metodzie Forda-Fulkersona sposób wyznaczania ścieżki powiększającej jest dowolny.
Pojęcia
Aby zrozumieć algorytm Edmondsa-Karpa (i ogólnie metodę Forda-Fulkersona) konieczna jest znajomość następujących pojęć:
- Sieć residualna – graf skierowany, w którym każdy łuk (krawędź skierowana) informuje, o ile można zmienić (zwiększyć bądź zmniejszyć) przepływ w danym łuku sieci przepływowej. Przykład: załóżmy, że w sieci przepływowej mamy łuk prowadzący z wierzchołka A do wierzchołka B o przepustowości 5, przy czym aktualnie wykorzystujemy przepustowość 2. Zakładamy też, że sieć nie zawiera łuku prowadzącego z B do A. W takim przypadku sieć residualna będzie zawierała łuk prowadzący z A do B o wartości 3 (o tyle możemy zwiększyć przepływ) oraz łuk prowadzący z B do A o wartości 2 (o tyle możemy zmniejszyć przepływ).
- Ścieżka powiększająca – ścieżka prosta (tzn. nie przechodząca wielokrotnie przez ten sam wierzchołek) w sieci residualnej prowadząca od źródła do ujścia.
- Przepustowość residualna ścieżki powiększającej – maksymalna wartość, o którą możemy zwiększyć przepływ na ścieżce powiększającej. Jest ona równa najmniejszej spośród wag łuków należących do ścieżki powiększającej.
Przebieg algorytmu
Algorytm ten przebiega w następująco:
- Tworzymy sieć residualną,
- Wyznaczamy ścieżkę powiększającą w sieci residualnej przeszukując ją wszerz,
- Jeśli nie da się wyznaczyć żadnej ścieżki powiększającej, kończymy działanie algorytmu. W przeciwnym razie modyfikujemy przepływ w sieci przepływowej o wartość residualną ścieżki powiększającej.
Złożoność czasowa algorytmu
Wyznaczenie ścieżki za pomocą przeszukiwania wszerz ma złożoność O(e) (e jest liczbą krawędzi). Liczba wykonań głównej pętli algorytmu jest rzędu O(ne) (n jest liczbą wierzchołków). Złożoność czasowa algorytmu Edmondsa-Karpa wynosi zatem O(ne2). Wyprowadzenie tych wartości można znaleźć w książce Wprowadzenie do algorytmów.
Bibliografia
- T.H. Cormen, Ch.E. Leiserson, R.L. Rivest, C. Stein, Wprowadzenie do algorytmów, Wydawnictwo Naukowe PWN, Warszawa, 2012.
- A. Debudaj-Grabysz, S. Deorowicz, J. Widuch, Algorytmy i struktury danych. Wybór zaawansowanych metod, Wydawnictwo Politechniki Śląskiej, Gliwice, 2012
Liczba głosów: 0.
- Algorytm Edmondsa-Karpa
- Metoda Forda-Fulkersona
- Metoda z zastosowaniem przepływu blokującego
Dodano: 22 listopada 2017 18:04, ostatnia edycja: 12 grudnia 2017 15:57.
Zobacz też
Sortowanie – zagadnienie polegające na uporządkowaniu elementów zbioru rosnąco lub malejąco według pewnego klucza. Zagadnienie to, ze względu na częstość występowania, jest bardzo istotne dla informatyki. Istnieje wiele różnych algorytmów realizujących sortowanie.
Programowanie dynamiczne – technika projektowania algorytmów polegająca na rozwiązywaniu podproblemów i zapamiętywaniu ich wyników. W technice tej, podobnie jak w metodzie dziel i zwyciężaj, problem dzielony jest na mniejsze podproblemy. Wyniki rozwiązywania podproblemów są jednak zapisywane w tabeli, dzięki czemu w przypadku natrafienia na ten sam podproblem nie trzeba go ponownie rozwiązywać.
Wykorzystując programowanie dynamiczne można zastosować metodę zstępującą z zapamiętywaniem lub metodę wstępującą.
- Metoda zstępująca z zapamiętywaniem polega na rekurencyjnym wywoływaniu funkcji z zapamiętywaniem wyników. Metoda ta jest podobna do metody dziel i zwyciężaj – różni się od niej tym, że jeśli rozwiązanie danego problemu jest już w tabeli z wynikami, to należy je po prostu stamtąd odczytać.
- Metoda wstępująca polega na rozwiązywaniu wszystkich możliwych podproblemów, zaczynając od tych o najmniejszym rozmiarze. Wówczas w momencie rozwiązywania podproblemu na pewno są już dostępne rozwiązania jego podproblemów. W tym podejściu nie zużywa się pamięci na rekurencyjne wywołania funkcji. Może się jednak okazać, że część podproblemów została rozwiązana nadmiarowo (nie były one potrzebne do rozwiązania głównego problemu).
Algorytm Johnsona – algorytm służący do wyznaczania najkrótszych ścieżek pomiędzy każdą parą wierzchołków w grafie. Algorytm wykorzystuje algorytm Dijkstry i algorytm Bellmana-Forda. Dopuszcza krawędzie o ujemnych wagach, o ile nie tworzą ujemnych cykli.
Złożoność czasowa algorytmu (jeśli algorytm Dijkstry zostanie zaimplementowany z wykorzystaniem kopca Fibonacciego) to O(n2log n + en), gdzie n jest liczbą wierzchołków, a e jest liczbą krawędzi. Dla grafów rzadkich (ze stosunkowo małą liczbą krawędzi) jest to złożoność lepsza, niż złożoność algorytmu Floyda-Warshalla.