Algorytmy genetyczne
Algorytm genetyczny – jedna z metaheurystyk inspirowanych biologiczną ewolucją.
Pojęcie algorytmu genetycznego nie jest powiązane z żadnym konkretnym problemem obliczeniowym, algorytm ten może być wykorzystywany do rozwiązywania różnych problemów. Algorytm genetyczny nie próbuje rozwiązywać problemu w sposób analityczny, ale próbuje uzyskać jak najlepsze rozwiązania poprzez wybieranie jak najlepszych cech rozwiązań z określonej puli. Implementując algorytm genetyczny należy przedstawić potencjalne rozwiązanie problemu w postaci jakiejś struktury danych, a następnie zdefiniować operacje krzyżowania, mutacji i selekcji. Zakładamy, że z każdym kolejnym pokoleniem rozwiązania występujące w populacji będą coraz lepsze.
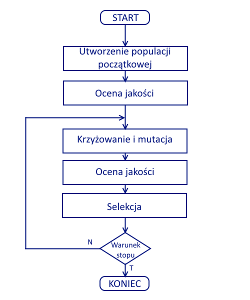
Operacje
Utworzenie populacji początkowej
Na początku działania algorytmu trzeba utworzyć populację początkową. Najczęściej polega to na utworzeniu pewnej liczby zupełnie losowych rozwiązań (określanych jako osobniki).
Sposób kodowania rozwiązania (osobnika) nie jest określony, zależy on od konkretnego problemu do rozwiązania. Klasycznym podejściem jest kodowanie binarne, czyli przedstawienie osobnika za pomocą ciągu zer i jedynek. Wówczas wartość 1 może oznaczać obecność jakiegoś elementu w rozwiązaniu, a 0 jej brak. Innym popularnym rozwiązaniem jest ciąg liczb naturalnych. Takie rozwiązanie znajduje zastosowanie między innymi w przypadku problemu komiwojażera, gdzie kolejność liczb oznacza kolejność odwiedzania punktów na trasie.
Ocena jakości
Algorytm genetyczny musi mieć funkcję oceny jakości rozwiązania pozwalającą określić, które rozwiązanie jest lepsze. Funkcja ta jest określana jako funkcja oceny lub funkcja przystosowania.
Krzyżowanie
Operacja krzyżowania polega na utworzeniu potomka (lub potomków) na podstawie dwóch wybranych elementów populacji. Potomek zawiera w sobie część cech jednego rodzica, a część drugiego. W przypadku kodowania binarnego najprostszym rozwiązaniem jest skopiowanie części ciągu z jednogo rodzica, a pozostałej części z drugiego. Jeśli osobniki zakodowane są za pomocą ciągu liczb, można stosować następującą metodę krzyżowania: część rozwiązania jest kopiowana z jednego rodzica, a następnie brakujące liczby są wstawiane w takiej kolejności, w jakiej wystąpowały w drugim rodzicu.
Mutacja
Operacja mutacji polega na dokonaniu losowej zmiany w którymś z osobników. Operacja ta powinna być stosowana stosunkowo rzadko (mutacji powinno podlegać znacznie mniej osobników, niż krzyżowaniu). W kodowaniu binarnym mutacją możę być zamiana losowego bitu na przeciwny, a w kodowaniu za pomocą ciągu liczb np. zamiana miejscami dwóch elementów.
Selekcja
Celem selekcji jest usunięcie z populacji rozwiązań słabych, a pozostawienie dobrych, które będą podlegały krzyżowaniu. W trywialnym przypadku może być zrealizowane po prostu przez pozostawienie określonej liczby najlepszych rozwiązań (osobników) i usunięcie pozostałych. Zazwyczaj selekcja jest bardziej złożona – prawdopodobieństwo zostania rodzicem zależy od oceny jakości osobnika, jednak nawet w przypadku słabych osobników nie jest ono zerowe.
Warunek stopu
Algorytm musi mieć zdefiniowany moment, w którym ma zakończyć swoje działanie. Najprostszym rozwiązaniem jest określenie liczby iteracji (pokoleń). Po zakończeniu działania algorytmu najlepszy osobnik z populacji jest zwracany jako wynik. Warunkiem stopu może być również ocena jakości najlepszego osobnika w populacji.
Zobacz też
Bibliografia
- A. Debudaj-Grabysz, S. Deorowicz, J. Widuch, Algorytmy i struktury danych. Wybór zaawansowanych metod, Wydawnictwo Politechniki Śląskiej, Gliwice, 2012, ISBN 9788373359383.
Liczba głosów: 3.
- Algorytmy genetyczne
- Algorytmy memetyczne
- Algorytmy zachłanne
- Symulowane wyżarzanie
Dodano: 1 maja 2017 18:57, ostatnia edycja: 7 czerwca 2023 18:41.
Zobacz też
Kolejka (ang. Queue) – struktura danych, w której elementy pobierane są z początku, a dodawane na końcu. Z kolejki można zatem pobrać tylko ten element, który był dodany najwcześniej. Kolejka bywa określana również jako kolejka FIFO (z ang. First In, First Out), w odróżnieniu od kolejki LIFO, czyli stosu.
Zanieczyszczenie Giniego (ang. Gini Impurity) – miara niejednorodności danego zbioru wyrażająca się wzorem:
$$G = ∑↙{n} p_n (1-p_n),$$gdzie pn jest prawdopodobieństwem przynależności elementu do klasy n, czyli liczbą elementów danej klasy podzieloną przez liczbę elementów całego zbioru. Jeśli wszystkie elementy zbioru należą do tej samej klasy, zanieczyszczenie Giniego jest równe 0.
Zanieczyszczenia Giniego nie należy mylić ze współczynnikiem Giniego. Są to miary służące do wyrażania zupełnie innych rzeczy. Współczynnik Giniego określa nierównomierność rozkładu i jest wykorzystywany między innymi do liczbowego wyrażania nierówności w dochodach danego społeczeństwa.
Stos (ang. Stack) – struktura danych, w której bezpośredni dostęp jest tylko do ostatnio dodanego elementu. Stos bywa określany także jako kolejka LIFO (z ang. Last In, First Out, czyli: ostatni na wejściu, pierwszy na wyjściu). Stos można sobie wyobrazić jako kilka rzeczy ułożonych „jedna na drugiej” – łatwo można wziąć tylko rzecz leżącą na samym wierzchu, gdyż pozostałe są przykryte.