Algorytmy memetyczne
Algorytm memetyczny – algorytm będący połączeniem algorytmu genetycznego i metod lokalnej optymalizacji. Czasami określany również jako hybrydowy algorytm ewolucyjny.
Różnice między algorytmem genetycznym a memetycznym
W algorytmie genetycznym zadanie w ogóle nie jest rozwiązywane w sposób analityczny – liczymy, że mechanizmy ewolucji same znajdą dobre rozwiązanie. W przypadku algorytmów memetycznych wzbogacamy to podejście o pewne elementy analityczne.
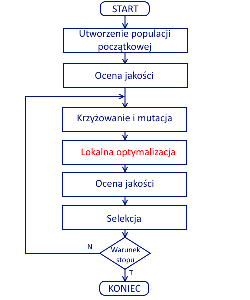
Algorytm memetyczny oprócz operacji krzyżowania, mutacji i selekcji ma również operację lokalnej optymalizacji. Celem tej operacji jest zmodyfikowanie osobnika populacji tak, aby osiągnąć lepsze rozwiązanie. Do modyfikacji tej wykorzystuje się wiedzę specjalistyczną dla danego zagadnienia.
Przykład
Załóżmy, że mamy algorytm genetyczny służący do rozwiązywania problemu komiwojażera (możemy przyjąć, że został zaimplementowany tak, jak w samouczku zamieszczonym na naszej stronie). Aby zrobić na jego podstawie algorytm memetyczny, musimy zaimplementować operację lokalnej optymalizacji. Operacja ta będzie umieszczona między krzyżowaniem a selekcją.
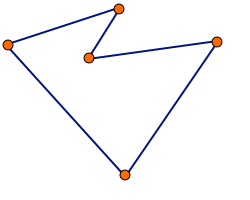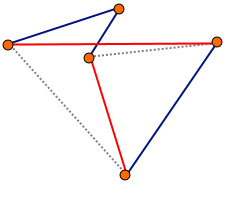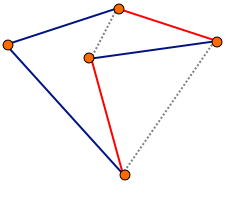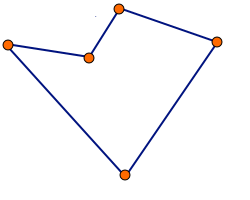
Jako operację lokalnej optymalizacji możemy przyjąć algorytm 2-optymalny. Algorytm ten polega na usunięciu z cyklu dwóch krawędzi i zastąpieniu ich innymi krawędziami (tak, aby nadal był prawidłowy cykl). Dla n wierzchołków mamy złożoność obliczeniową o(n2). Po sprawdzeniu wszystkich par krawędzi wybieramy tę zamianę, która powoduje największe skrócenie trasy. Jeśli żadna z modyfikacji nie spowodowała skrócenia trasy, zostawiamy rozwiązanie pierwotne.
Elementy analityczne można również wprowadzić do generowania populacji początkowej. Oprócz rozwiązań zupełnie losowych, mogą się tam znaleźć rozwiązania wyznaczone za pomocą prostego algorytmu heurystycznego, jak np. algorytm najbliższego sąsiada.
Bibliografia
- Yew-Soon O., Meng-Hiot L., Ning Z., Kok-Wai W., Classification of Adaptive Memetic Algorithms: A Comparative Study, IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), Volume 36, Issue 1, 2006, s. 141-152, DOI: 10.1109/TSMCB.2005.856143.
- D.S. Johnson, L.A. McGeoch, The Traveling Salesman Problem: A Case Study in Local Optimization, 1995 [Dostęp 2019-01-26].
Liczba głosów: 0.
- Algorytmy genetyczne
- Algorytmy memetyczne
- Algorytmy zachłanne
- Symulowane wyżarzanie
Dodano: 3 czerwca 2017 11:15, ostatnia edycja: 1 maja 2020 16:13.
Zobacz też
Przeszukiwanie w głąb (ang. depth-first search, w skrócie DFS) – jeden z dwóch podstawowych algorytmów przeszukiwania grafu. Polega na przechodzeniu zawsze do kolejnego nieodwiedzonego wierzchołka. Jeśli dany wierzchołek nie ma nieodwiedzonych sąsiadów, wracamy do poprzedniego wierzchołka i sprawdzamy jego sąsiadów. Mówiąc obrazowo, w algorytmie tym wchodzimy tak głęboko, jak to możliwe (przechodzimy dalej, dopóki się da).
Algorytm można zapisać w sposób rekurencyjny. Wywoływana rekurencyjnie procedura działa następująco: oznacz wierzchołek jako odwiedzony, a następnie wywołaj tę procedurę dla każdego sąsiada danego wierzchołka, jeśli nie został on wcześniej odwiedzony. Na początku wywołujemy procedurę dla wierzchołka początkowego.
Ten artykuł opisuje algorytm rozwiązujący problem wydawania reszty oparty na programowaniu dynamicznym. Algorytm ten daje gwarancję znalezienia rozwiązania optymalnego.
Istnieje również pewna modyfikacja tego algorytmu, która została opisana w osobnym artykule.
2-opt, algorytm 2-optymalny – algorytm lokalnej optymalizacji wykorzystywany przy rozwiązywaniu problemu komiwojażera. Jest to szczególny przypadek algorytmu k-optymalnego.
Algorytm 2-opt nie służy do wyznaczania trasy, a jedynie do ulepszania jej. Samą trasę można wyznaczyć np. za pomocą algorytmu najbliższego sąsiada. Algorytm może być wykorzystany do ulepszenia algorytmu genetycznego – w ten sposób powstanie algorytm memetyczny.