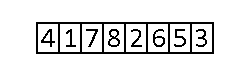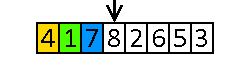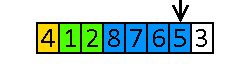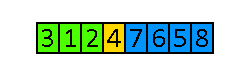Quicksort, sortowanie szybkie – algorytm sortowania działający w średnim przypadku w czasie liniowo-logarytmicznym. Algorytm jest oparty na metodzie dziel i zwyciężaj. Nie jest to algorytm stabilny ani wykazujący zachowanie naturalne, jednak ze względu na efektywność jest algorytmem bardzo popularnym.

Przebieg algorytmu

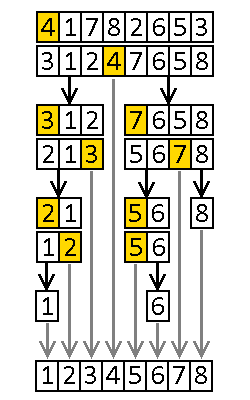
Quicksort jest algorytmem rekurencyjnym, jego działanie można opisać następująco:

• Wybierz jeden z elementów jako klucz osiowy,
• Przenieś wszystkie elementy mniejsze od klucza osiowego na jedną stronę tablicy, a pozostałe na drugą,
• Wywołaj procedurę rekurencyjnie dla części tablicy na lewo od klucza osiowego i na prawo od klucza osiowego.

Wybór klucza osiowego może być dowolny, jednak powinien być jak najszybszy. W praktyce często stosuje się po prostu wybór pierwszego elementu.

Operacja przerzucania elementów powinna musi być zaimplementowana tak, aby wykonywała się w czasie liniowym. Przykładowo, może ona być zdefiniowana w następujący sposób:

• Przyjmujemy pierwszy element za klucz osiowy.
• Dla każdego kolejnego elementu:
  • Jeśli jest większy od klucza osiowego, zostawiamy go na miejscu.
  • W przeciwnym razie zamieniamy go miejscami z pierwszym elementem większym od klucza osiowego (wyjątek: jeśli nie znaleźliśmy wcześniej żadnego elementu większego od klucza osiowego, nie robimy nic).
• Zamieniamy miejscami klucz osiowy z ostatnim elementem mniejszym od niego.

REKLAMA

Analiza algorytmu

Jak już wspomniano, operacja przenoszenia elementów odbywa się w czasie liniowym. O złożoności algorytmu decyduje więc to, ile nastąpi rekurencyjnych wywołań funkcji. W przypadku optymistycznym tablica będzie dzielona na pół. Wówczas głębokość drzewa wywołań zależy logarytmicznie od liczby danych wejściowych, czyli optymistyczna złożoność czasowa algorytmu jest rzędu O(n logn). Możemy wykazać, że taki sam rząd złożoności wystąpi w przypadku średnim (dowód jest dostępny w książkach podanych w bibliografii).

Przypadek pesymistyczny występuje wtedy, gdy klucz osiowy za każdym razem znajdzie się na brzegu tabeli. Wówczas przy każdym kolejnym wywołaniu liczba elementów do posortowania jest tylko o 1 mniejsza, zatem funkcja zostanie wywołana n razy. Pesymistyczna złożoność czasowa wynosi zatem O(n²).

Przeanalizujmy złożoność pamięciową algorytmu. Sortowanie szybkie nie potrzebuje co prawda dodatkowej pamięci na przechowywanie sortowanych danych, wymaga jednak pamięci potrzebnej na obsługę rekurencyjnych wywołań funkcji. Rozmiar tej pamięci (podobnie jak czas wykonania) będzie zależał od głębokości drzewa wywołań. Złożoność pamięciowa wynosi więc O(logn) w przypadku średnim i O(n) w przypadku pesymistycznym. Nie jest to zatem algorytm sortujący w miejscu.

Zastanówmy się, kiedy może wystąpić przypadek pesymistyczny. Jeśli jako klucz osiowy obieramy pierwszy (lub ostatni) elementu z tablicy, to najgorszy przypadek wystąpi wtedy, gdy tablica jest już posortowana. Widzimy więc, że algorytm zachowuje się w sposób bardzo nienaturalny.

Możliwe usprawnienia

Niedoskonałości algorytmu można nieco poprawić stosując następujące techniki:

• Jako klucz osiowy zamiast pierwszego elementu można obierać element losowy. Nie zmieni to złożoności algorytmu, jednak sprawi, że przypadek pesymistyczny nie będzie występował w przypadku tablicy posortowanej.
• Przy wyborze klucza osiowego można zastosować nieco bardziej złożone techniki. Jednym z rozwiązań jest wybór mediany z kilku wybranych elementów (np. pierwszego, ostatniego i środkowego). Należy jednak uważać, żeby nie spowolniło to zbytnio całej procedury – siła omawianego algorytmu tkwi w tym, aby wybór klucza osiowego i przestawianie elementów było jak najszybsze.
• W celu zmniejszenia liczby rekurencyjnych wywołań funkcji, dla małych tablic można zastosować jakiś prosty, nierekurencyjny algorytm sortowania, np. sortowanie przez wstawianie (wówczas mamy do czynienia z algorytmem hybrydowym).
• Jeśli wartość klucza osiowego powtarza się w tablicy, można od razu ustawić te elementy obok klucza osiowego i nie włączać tego fragmentu tablicy do wywołań rekurencyjnych. Taka modyfikacja jest określana jako Quick Sort 3 Way Partition.

Kod źródłowy

Przykładowa implementacja algorytmu w języku C wygląda następująco:

void quicksort(int* tab, int poczatek, int n)
{
    if (n > 1) 
    {
        int liczba_mniejszych = 0;
        int liczba_wiekszych = 0;
        
        int koniec = poczatek + n;
        int t; // Zmienna tymczasowa
    
        // Przeniesienie elementow wokol klucza osiowego
        for (int i = (poczatek + 1); i < koniec; ++i)
        {
            
            if (tab[i] < tab[poczatek])
            {   
                if (liczba_wiekszych > 0)
                {
                    // Przeniesienie elementu mniejszego od klucza osiowego
                    // przed elementy wieksze od klucza osiowego
                    t = tab[poczatek+liczba_mniejszych+1];
                    tab[poczatek+liczba_mniejszych+1] = tab[i];
                    tab[i] = t;
                }                    
                ++liczba_mniejszych; 
            }
            else
            {
                ++liczba_wiekszych;
            }
            
        }
        
        // Wstawienie klucza osiowego na wlasciwe miejsce
        t = tab[poczatek+liczba_mniejszych];
        tab[poczatek+liczba_mniejszych] = tab[poczatek];
        tab[poczatek] = t;
        
        // Wywołanie rekurencyjne
        quicksort(tab, poczatek, liczba_mniejszych);
        quicksort(tab, koniec-liczba_wiekszych, liczba_wiekszych);
        
    }
}

// Przykladowe uzycie funkcji
int main()
{
    int tab[] = {3, 7, 5, 1, 5, 8, 4, 2};
    quicksort(tab, 0, 8);
    
    return 0; 
}

REKLAMA

Bibliografia

• T.H. Cormen, Ch.E. Leiserson, R.L. Rivest, C. Stein, Wprowadzenie do algorytmów, Wydawnictwo Naukowe PWN, Warszawa, 2012, ISBN 9788301169114.
• Z.J. Czech, S. Deorowicz, P. Fabian, Algorytmy i struktury danych. Wybrane zagadnienia, Wydawnictwo Politechniki Śląskiej, Gliwice, 2010, ISBN 9788373356689.
• Quick Sort (3 Way Partition) - Sorting Algorithm Animations, toptal.com [Dostęp 2019-01-30].