Sortowanie przez scalanie

Sortowanie przez scalanie – rekurencyjny algorytm sortowania wykorzystujący metodę dziel i zwyciężaj.

Działanie algorytmu

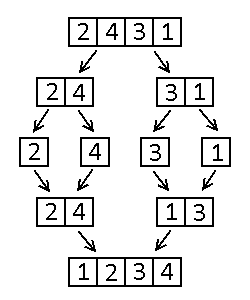
Sortowanie przez scalanie przebiega następująco:

• Jeśli rozmiar tablicy do posortowania wynosi 1, nic nie rób (tablica jest już posortowana).
• W przeciwnym razie:
  • Posortuj pierwszą połowę tablicy.
  • Posortuj drugą połowę tablicy.
  • Scal otrzymane wyniki.

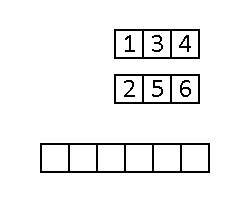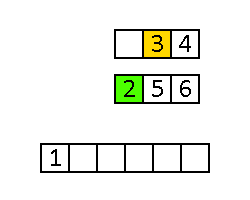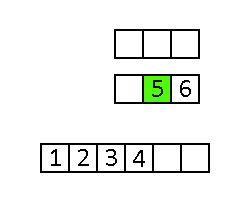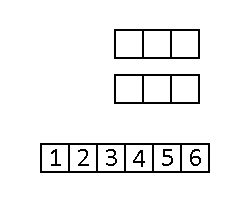
Operacja scalania polega na porównywaniu pierwszych elementów posortowanych podtablic i przenoszeniu mniejszego z nich (lub większego, jeśli sortujemy malejąco) do nowej tablicy. Jeśli w jednej z podtablic nie ma już elementów, trzeba kolejno przenosić do tablicy z wynikami kolejne elementy drugiej.

Złożoność obliczeniowa

Głębokość drzewa wywołań funkcji dla tablicy o rozmiarze n wynosi log₂n (zaokrąglone w górę). Złożoność operacji scalania tablic jest liniowa. Złożoność czasowa algorytmu jest zatem O(nlogn).

W pamięci operacyjnej potrzebne jest miejsce na obsługę kolejnych wywołań funkcji oraz na tymczasowe tablice potrzebne przy scalaniu. Złożoność pamięciowa algorytmu jest rzędu O(n).

Ocena algorytmu

Algorytm ma mniejszą złożoność czasową niż proste algorytmy, takie jak np. sortowanie bąbelkowe czy sortowanie przez wstawianie. W zamian za to ma jednak gorszą złożoność pamięciową.

Dodatkową zaletą sortowania przez scalanie jest to, że algorytm ten można zrównoleglić. Poszczególne podtablice można sortować niezależnie od siebie, zatem sortowania te można wykonywać w osobnych wątkach.

Przykładowa implementacja w języku C++

Przykładowy kod źródłowy w języku C++ jest umieszczony poniżej. Kod ten realizuje sortowanie rosnące.

void sortowanie_przez_scalanie(int* tab, int n)
{
    if (n > 1) 
    {
        int n1 = n/2;
        int n2 = n - n1;
        
        // Wywolanie rekurencyjne
        sortowanie_przez_scalanie(tab, n1);  
        sortowanie_przez_scalanie(&tab[n1], n2);
    
        //Przepisanie wynikow do tymczasowych tablic
        int i;
        
        int* tab1 = new int[n1];
        int* tab2 = new int[n2];

        for (i = 0; i < n1; ++i)
        {
            tab1[i] = tab[i];
        } 
        for (i = n1; i < n; ++i)
        {
            tab2[i-n1] = tab[i];
        }
    
        // Scalenie
        int in1, in2;
        in1 = in2 = 0;
        
        for (i = 0; i < n; ++i) 
        {
            if ((in1 < n1) && (tab1[in1] <= tab2[in2]))
            {
                tab[i] = tab1[in1];
                ++in1;
            }
            else
            {
                tab[i] = tab2[in2];
                ++in2;
            }                     
        }
    
        delete[] tab1;
        delete[] tab2;
    }
}

Bibliografia

1. T.H. Cormen, Ch.E. Leiserson, R.L. Rivest, C. Stein, Wprowadzenie do algorytmów, Wydawnictwo Naukowe PWN, Warszawa, 2012.