Plik: Stos
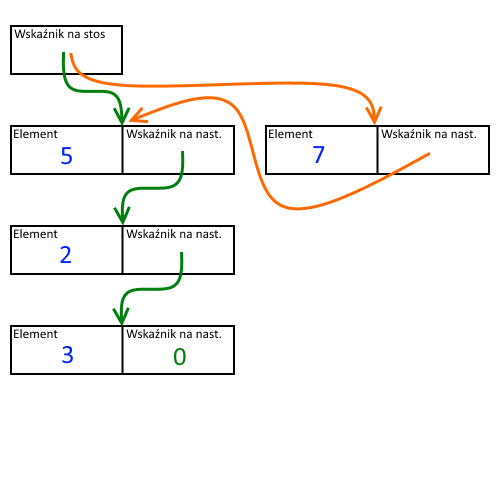
Dodano: 13 kwietnia 2018 19:44.
Wykorzystanie pliku w artykułach:Zobacz też
Algorytm memetyczny – algorytm będący połączeniem algorytmu genetycznego i metod lokalnej optymalizacji. Czasami określany również jako hybrydowy algorytm ewolucyjny.
Przeszukiwanie w głąb (ang. depth-first search, w skrócie DFS) – jeden z dwóch podstawowych algorytmów przeszukiwania grafu. Polega na przechodzeniu zawsze do kolejnego nieodwiedzonego wierzchołka. Jeśli dany wierzchołek nie ma nieodwiedzonych sąsiadów, wracamy do poprzedniego wierzchołka i sprawdzamy jego sąsiadów. Mówiąc obrazowo, w algorytmie tym wchodzimy tak głęboko, jak to możliwe (przechodzimy dalej, dopóki się da).
Algorytm można zapisać w sposób rekurencyjny. Wywoływana rekurencyjnie procedura działa następująco: oznacz wierzchołek jako odwiedzony, a następnie wywołaj tę procedurę dla każdego sąsiada danego wierzchołka, jeśli nie został on wcześniej odwiedzony. Na początku wywołujemy procedurę dla wierzchołka początkowego.
2-opt, algorytm 2-optymalny – algorytm lokalnej optymalizacji wykorzystywany przy rozwiązywaniu problemu komiwojażera. Jest to szczególny przypadek algorytmu k-optymalnego.
Algorytm 2-opt nie służy do wyznaczania trasy, a jedynie do ulepszania jej. Samą trasę można wyznaczyć np. za pomocą algorytmu najbliższego sąsiada. Algorytm może być wykorzystany do ulepszenia algorytmu genetycznego – w ten sposób powstanie algorytm memetyczny.






