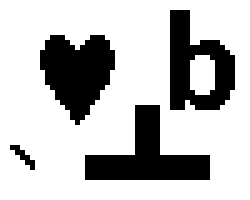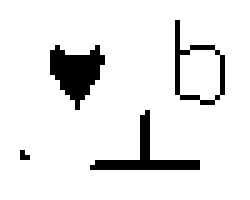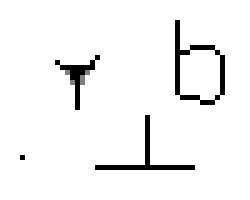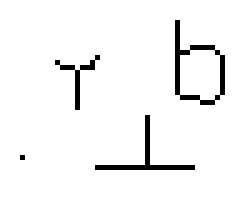Algorytm Zhanga-Suena
Algorytm Zhanga-Suena – algorytm służący do szkieletyzacji obrazu binarnego. Szkieletyzacja polega na wyborze z obrazu binarnego tych pikseli, które są równo odległe od krawędzi obiektu.
Przebieg algorytmu
Przyjmijmy, że w przetwarzanym obrazie binarnym piksele o wartości 0 są pikselami tła, a piksele o wartości 1 są pikselami obiektów. Algorytm Zhanga-Suena jest algorytmem iteracyjnym – w każdej iteracji dla każdego piksela obiektów podejmowana jest decyzja, czy piksel ten należy usunąć, czy zostawić. Przy podjęciu decyzji brane jest pod uwagę sąsiedztwo piksela liczące 8 pikseli (sąsiedztwo Moore'a). Niech piksel P1 będzie aktualnie analizowanym pikselem. Jego sąsiedztwo oznaczone jest następująco:
| P9 | P2 | P3 |
| P8 | P1 | P4 |
| P7 | P6 | P5 |
Dla analizowanego piksela P1 najpierw należy wyznaczyć następujące wartości:
- B(P1) – liczba pikseli o wartości 1 w sąsiedztwie piksela,
- A(P1) – liczba przejść 01 w ciągu (P2, P3, P4, P5, P6, P7, P8, P9, P2).
- 2 ≤ B(P1) ≤ 6,
- A(P1) = 1,
- (P2×P4×P6)+(P4×P6×P8)=0.
- (P2×P4×P8)+(P2×P6×P8)=0.
Należy pamiętać, że w każdej iteracji obraz należy zmodyfikować dopiero po przeanalizowaniu wszystkich pikseli – jeśli podjęto decyzję o usunięciu piksela, to do zakończenia danej iteracji dla jego sąsiadów musi on być nadal traktowany jako piksel o wartości 1. Można to zagwarantować np. tworząc na początku iteracji kopię obrazu, aby sprawdzać wartość pikseli w kopii, a modyfikować oryginał.
Algorytm kończy swoje działanie, gdy w trakcie dwóch ostatnich iteracji nie został usunięty żaden piksel.
Aby uniknąć błędów związanych z odczytem spoza obrazu, nie można analizować pikseli znajdujących się przy samej krawędzi. Z tego powodu dobrze jest zapewnić, że żaden piksel obiektu nie leży na krawędzi obrazu. Przykładowo, można przed rozpoczęciem działania algorytmu dodać do obrazu z każdej strony krawędź o szerokości jednego piksela zawierającą tylko piksele tła.
Komentarze
Warunek B(P1)≥2 zabezpiecza przed usunięciem ostatniego piksela w linii. Warunek B(P1)≤6 zabezpiecza przed wycinaniem dziur wewnątrz obiektów. Warunek A(P1)=1 zabezpiecza przed usunięciem piksele należące do szkieletu (sąsiadujące z tłem z więcej niż jednej strony). Dzięki trzeciemu warunkowi (zmieniającemu się pomiędzy iteracjami) w przypadku idealnie pionowych lub poziomych bloków ścinana jest naprzemiennie jedna i druga krawędź, co zabezpiecza przez powstaniem dziur w szkielecie (nie ma ryzyka, że dwa piksele pośrodku bloku zostaną usunięte w tej samej iteracji).
Algorytm ma pewne mankamenty. Przykładowo, w wyniku jego działania usunięte zostaną kwadraty o wymiarach 2×2. Innym problemem jest przycięcie niektórych ukośnych linii do pojedynczego piksela – taki przypadek przedstawiono w lewym dolnym rogu animacji (1).
Algorytm został opublikowany w pracy [1]. Przykładowe implementacje algorytmu są dostępne na stronie [2].
Bibliografia
- T.Y. Zhang, C.Y. Suen, A Fast Parallel Algorithm for Thinning Digital Patterns, Magazine Communications of the ACM, Volume 27, Issue 3, 1984, s. 236-239, DOI: 10.1145/357994.358023.
- Zhang-Suen thinning algorithm, rosettacode.org [Dostęp 2019-02-02].
Liczba głosów: 0.
- Algorytm Zhanga-Suena
- Metoda Otsu
Dodano: 2 lutego 2019 15:18, ostatnia edycja: 21 kwietnia 2020 17:38.
Zobacz też
Wyznaczanie najkrótszej ścieżki – zagadnienie polegające na wyszkaniu w grafie takiej ścieżki łączącej dwa wierzchołki, której suma wag krawędzi jest jak najmniejsza.
W przypadku pesymistycznym do wyznaczenia optymalnej ścieżki z wierzchołka A do wierzchołka B konieczne jest wyznaczenie najkrótszych ścieżek z wierzchołka A do wszystkich pozostałych wierzchołków w grafie. Zagadnienie takie jest określane jako poszukiwanie najkrótszych ścieżek z jednego źródła. Do rozwiązywania tego zagadnienia można wykorzystać następujące algorytmy:
Nieco innym zagadnieniem jest poszukiwanie najkrótszych ścieżek pomiędzy każdą parą wierzchołków. W tym celu można wykorzystać algorytmy wymienione powyżej (wykonując je wielokrotnie, za każdym razem przyjmując inny wierzchołek źródłowy) lub algorytmy poszukujące od razu wszystkich ścieżek, takie jak:
Aby znalezienie najkrótszej ścieżki było możliwe, graf nie może zawierać ujemnych cykli osiągalnych z wierzchołka źródłowego. Jeśli taki cykl istnieje, to poruszając się nim „w kółko” cały czas zmniejszamy długość ścieżki. Dopuszczalne jest natomiast występowanie krawędzi o ujemnej wadze, choć nie wszystkie algorytmy dopuszczają ten przypadek.
Jeśli poszukujemy ścieżek o najmniejszej liczbie krawędzi (np. wtedy, gdy wszystkie krawędzie mają taką samą, dodatnią wagę), to zamiast powyższych algorytmów możemy skorzystać z prostego przeszukiwania grafu wszerz.
Metoda Forda-Fulkersona – algorytm służący do wyznaczania maksymalnego przepływu. Jest to algorytm bardzo ogólny, dlatego często nie jest nazywany algorytmem, a metodą. Popularną implementacją tej metody jest algorytm Edmondsa-Karpa. Algorytm można opisać następująco:
- Wyznacz sieć residualną (opis sieci residualnej znajduje się w dalszej części artykułu).
- Znajdź w sieci residualnej dowolną ścieżkę powiększającą.
- Jeśli nie udało się wyznaczyć żadnej ścieżki powiększającej, zakończ działanie algorytmu.
- W przeciwnym razie zwiększ przepływ w sieci (w sposób opisany w dalszej części artukułu) i wróć do punktu 1.
Graf – struktura G = (V, E) składająca się ze skończonego zbioru wierzchołków V oraz skończonego zbioru krawędzi E, gdzie każda krawędź e ∈ E jest dwuelementowym zbiorem wierzchołków u, v ∈ V. Wierzchołki u, v połączone krawędzią e = {u, v} określane są sąsiednimi. Grafy mają szerokie zastosowanie w informatyce, można za ich pomocą przedstawiać rożnego rodzaju relacje pomiędzy obiektami.
Powyższa definicja dotyczy grafu nieskierowanego, gdzie relacja sąsiedztwa jest symetryczna, tzn. krawędź łączy wierzchołki „w obie strony”. W grafie skierowanym krawędzie są „jednokierunkowe”. Krawędź grafu skierowanego zazwyczaj jest określana jako łuk.
Graf ważony (inaczej graf z wagami) to taki graf, w którym każdej krawędzi przypisana jest pewna wartość liczbowa. Wartość ta może oznaczać np. długość krawędzi lub jej przepustowość.