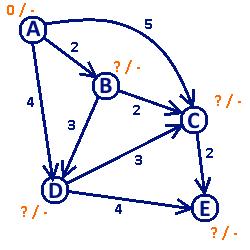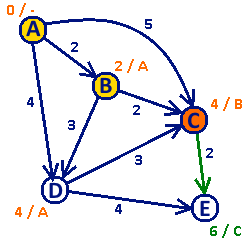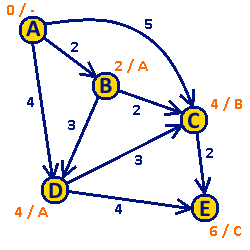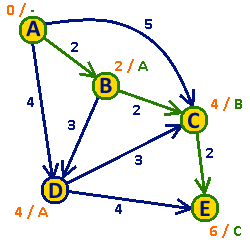
Plik: Algorytm Dijkstry animacja
Dodano: 24 marca 2017 13:51.
Wykorzystanie pliku w artykułach:Zobacz też
Metoda z zastosowaniem przepływu blokującego – algorytm wyznaczający maksymalny przepływ w sieci przepływowej. W algorytmie tym przepływ zwiększany jest iteracyjnie, w każdej iteracji wyznaczony przepływ jest powiększany o przepływ blokujący w warstwowej sieci residualnej.
K-opt, algorytm k-optymalny – algorytm lokalnej optymalizacji wykorzystywany przy rozwiązywaniu problemu komiwojażera. Algorytm ten nie służy do samego wyznaczania trasy, a jedynie do ulepszania jej. Najprostszą wersją tego algorytmu jest algorytm 2-optymalny.
Metoda Forda-Fulkersona – algorytm służący do wyznaczania maksymalnego przepływu. Jest to algorytm bardzo ogólny, dlatego często nie jest nazywany algorytmem, a metodą. Popularną implementacją tej metody jest algorytm Edmondsa-Karpa. Algorytm można opisać następująco:
- Wyznacz sieć residualną (opis sieci residualnej znajduje się w dalszej części artykułu).
- Znajdź w sieci residualnej dowolną ścieżkę powiększającą.
- Jeśli nie udało się wyznaczyć żadnej ścieżki powiększającej, zakończ działanie algorytmu.
- W przeciwnym razie zwiększ przepływ w sieci (w sposób opisany w dalszej części artukułu) i wróć do punktu 1.






