Problem wydawania reszty (ang. change-making problem) – problem obliczeniowy polegający na tym, aby mając określony zbiór nominałów wyrazić daną kwotę za pomocą jak najmniejszej liczby monet. Jest to szczególny przypadek problemu plecakowego.

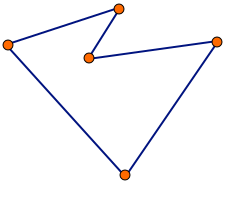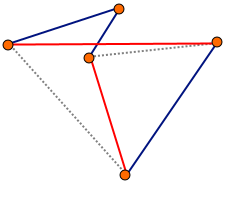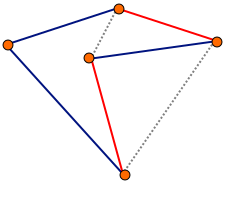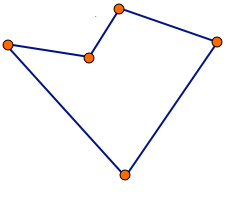
Algorytm Helda-Karpa (czasami określany jako algorytm Bellmana-Helda-Karpa) – algorytm służący do rozwiązywania problemu komiwojażera. Jest to algorytm dokładny oparty na programowaniu dynamicznym. Algorytm ma złożoność czasową O(n²2ⁿ) i złożoność pamięciową O(n2ⁿ). Jest to co prawda złożoność gorsza od wielomianowej, ale algorytm ten jest znacznie lepszy od algorytmu sprawdzającego wszystkie warianty (złożoność czasowa O(n!)).

Algorytm Johnsona – algorytm służący do wyznaczania najkrótszych ścieżek pomiędzy każdą parą wierzchołków w grafie. Algorytm wykorzystuje algorytm Dijkstry i algorytm Bellmana-Forda. Dopuszcza krawędzie o ujemnych wagach, o ile nie tworzą ujemnych cykli.

Złożoność czasowa algorytmu (jeśli algorytm Dijkstry zostanie zaimplementowany z wykorzystaniem kopca Fibonacciego) to O(n²log n + en), gdzie n jest liczbą wierzchołków, a e jest liczbą krawędzi. Dla grafów rzadkich (ze stosunkowo małą liczbą krawędzi) jest to złożoność lepsza, niż złożoność algorytmu Floyda-Warshalla.